1.2.7. Логическое следствие
Логическое следствие обозначают* значком 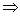 и
тоже читают «следовательно», «из этого следует это». Но это не то же самое, что импликация. и
тоже читают «следовательно», «из этого следует это». Но это не то же самое, что импликация.
* Импликацию тоже зачастую обозначают так, что вызывает путаницу
В чём отличие? Когда мы решаем задачу и пишем, что 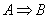 («из а следует бэ»), то полагаем высказывание («из а следует бэ»), то полагаем высказывание 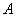 заведомо истинным и более того, выводим из него другую истину заведомо истинным и более того, выводим из него другую истину 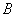 . В математической логике это и называется логическим
следствием. Обычно следствие . В математической логике это и называется логическим
следствием. Обычно следствие 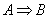 подлежит обоснованию, и поэтому
при оформлении работ всегда старайтесь пояснять, какие аксиомы, теоремы, решённые задачи и т. д. вы использовали для того или иного
вывода. подлежит обоснованию, и поэтому
при оформлении работ всегда старайтесь пояснять, какие аксиомы, теоремы, решённые задачи и т. д. вы использовали для того или иного
вывода.
Теорема по своей сути тоже представляет собой логическое следствие: её условие опирается на истинные посылки 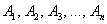 (аксиомы, уже доказанные теоремы). Доказательство же
устанавливает истинность следствия (аксиомы, уже доказанные теоремы). Доказательство же
устанавливает истинность следствия 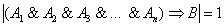 , причём в этом процессе не
могут использоваться ложные рассуждения. , причём в этом процессе не
могут использоваться ложные рассуждения.
Недоказанное предположение называют гипотезой, и варианта тут два: либо она выводит из истины истину и представляет собой теорему, либо
гипотеза оказывается неверной, т. е. из множества истинных посылок 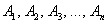 следует «не бэ», и это
истина: следует «не бэ», и это
истина: 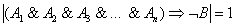 . В случае опровержения получается тривиальный вывод
«это неверно», но и то, бывает, дорогого стОит. . В случае опровержения получается тривиальный вывод
«это неверно», но и то, бывает, дорогого стОит.
Рассмотрим в качестве примера, конечно, не мегатеорему, но утверждение, которое требует пусть простого, но обоснования. Хотя и его не
будет:) Итак, есть высказывания:
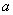 – число делится на 4, – число делится на 4,
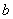 – число делится на 2. – число делится на 2.
Очевидно, что следствие 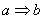 истинно, то есть из того, что
число делится на 4, следует и его делимость на 2. И, соответственно, противоположное заключение – есть ложь: истинно, то есть из того, что
число делится на 4, следует и его делимость на 2. И, соответственно, противоположное заключение – есть ложь: 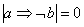
При этом ещё раз обращаю внимание, что посылка 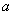 изначально постулируется как истина (в отличие от импликации, где она
может быть и ложной). Для логических следствий имеют место такие же понятия необходимости и достаточности: изначально постулируется как истина (в отличие от импликации, где она
может быть и ложной). Для логических следствий имеют место такие же понятия необходимости и достаточности:
истинность посылки 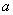 – это достаточное условие для
истинности заключения – это достаточное условие для
истинности заключения 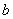 , ,
истинность заключения 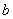 – это необходимое условие для
истинности посылки – это необходимое условие для
истинности посылки 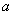 . .
В нашем примере:
Делимость числа на 4 является достаточным условием для того, чтобы оно делилось на 2. И с другой стороны, делимость числа на 2
является необходимым условием делимости на 4 (но не достаточным! – так, например, число 6 прекрасно делится на 2, но не делится на
4).
Следует отметить, что рассмотренный пример можно записать и в виде импликации: 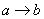 (пользуясь таблицей, проанализируйте все расклады
самостоятельно) (пользуясь таблицей, проанализируйте все расклады
самостоятельно)
Однако в общем случае «перенос понятий» некорректен! То есть, если мы ведём разговор о том, что 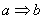 , то это ещё не значит, что будет справедлива импликация , то это ещё не значит, что будет справедлива импликация 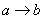 . И такой пример будет позже. . И такой пример будет позже.
 1.2.8. Эквиваленция. Необходимое и достаточное условие 1.2.8. Эквиваленция. Необходимое и достаточное условие
 1.2.6. Импликация. Необходимое условие. Достаточное условие 1.2.6. Импликация. Необходимое условие. Достаточное условие
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих 1.2.8. Эквиваленция. Необходимое и достаточное условие
1.2.8. Эквиваленция. Необходимое и достаточное условие 1.2.6. Импликация. Необходимое условие. Достаточное условие
1.2.6. Импликация. Необходимое условие. Достаточное условие