|
Ваш репетитор, справочник и друг!
|
2.2. Выражения с комплексными числамиВыше мы изучили отдельные арифметические действия с комплексными числами: сложение, умножение и так далее. Но на практике эти действия часто комбинируются, в результате чего получается целое выражение с комплексными числами: Пример 19 Даны комплексные числа Выполнить следующие действия: Решение: для комплексных чисел работает «обычный» алгебраический порядок действий. Сначала выполняется умножение /
деление, затем – сложение /вычитание: Скобки меняют порядок действий (сначала выполняем, то, что в скобках): Если число находится в степени / под корнем, то эти действия имеют более высокий приоритет, нежели сложение / вычитание и умножение /
деление: Если под степенью находится выражение, то во многих случаях сначала удобнее вычислить его: Ответ: Разминаемся самостоятельно: Пример 20 Даны комплексные числа Вычислить …Никто не запутался? ;) Тогда приступаем к более содержательным заданиям: Пример 21 Упростить выражение Решение: итак, требуется подставить Как лучше оформить решение? С «навороченным» алгебраическим выражением удобнее разбираться поэтапно. Во-первых, меньше рассеивается внимание, и, во-вторых, если-таки задание не зачтут, то будет намного проще отыскать ошибку. 1) Сначала упростим числитель. Подставим в него значение 2) Теперь на очереди знаменатель. Если Заметьте, в какой непривычной редакции использована формула квадрата суммы 3) И, наконец, всё выражение. Если Чтобы избавиться от дроби, умножим числитель и знаменатель на сопряженное знаменателю число:
А сейчас ключевое правило, которое, вы, наверное, уже прочувствовали:
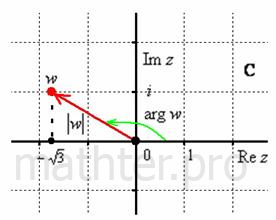
НИ В КОЕМ СЛУЧАЕ НЕ ТОРОПИМСЯ! Обозначим наше достижение буквой Вычислим модуль комплексного числа: Найдём аргумент. Так как число расположено во 2-й координатной четверти Таким образом: Выполним проверку:
Напоминаю, что «стандартные» значения синуса и косинуса удобно находить по Таблице значений тригонометрических функций (см. Приложение Тригонометрические таблицы). Если вы не помните её наизусть, конечно. Ответ: Аналогичный пример для самостоятельного решения: Пример 22 Упростить выражение Не пропускаем учебные примеры!! Кажутся-то они, может быть, и простыми, но без тренировки «сесть в лужу» не просто легко, а очень легко. Поэтому «набиваем руку». Решение для сверки в конце книги. Нередко задача допускает не единственный путь решения: Пример 23 Вычислить Решение: прежде всего, обратим внимание на оригинальное условие – одно число представлено в алгебраической, а другое – в тригонометрической форме, да
ещё и с градусами. Давайте сразу перепишем его в более привычном виде: Как решить предложенное выражение? В принципе, здесь можно раскрыть скобки
В результате: Используем правило умножения комплексных чисел в тригонометрической форме: если В нашем случае: Далее применяем формулу Муавра Делая дробь правильной: ответ: Но для «красоты» либо по требованию ответ легко перевести в алгебраическую форму: Следует заметить, что в этой задаче можно было сначала перевести второе число в алгебраическую форму Самостоятельно: Пример 24 Упростить выражение Здесь нужно вспомнить ходовые действия со степенями (на всякий случай включил в Приложение Горячие формулы), в
частности И ещё одно важное замечание: этот пример можно решить в двух стилях. С формальной точки зрения без разницы, как решать, но содержательное отличие есть! Пожалуйста, хорошо осмыслите вышесказанное: Краткое решение и ответ в конце книги. Выражения – хорошо, а уравнения – лучше:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих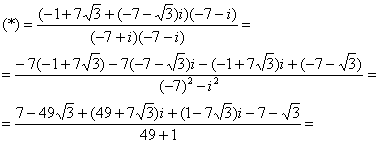
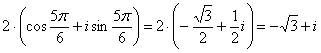 , в чём и требовалось убедиться.
, в чём и требовалось убедиться.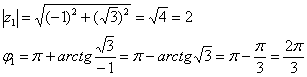
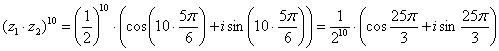
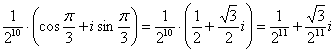 .
.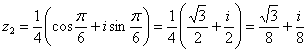 , выполнить умножение в алгебраической форме, затем перевести результат
, выполнить умножение в алгебраической форме, затем перевести результат 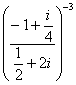
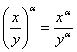 .
.  2.3. Уравнения с комплексными числами
2.3. Уравнения с комплексными числами 2.1.7. Извлечение корней из комплексных чисел
2.1.7. Извлечение корней из комплексных чисел