2.1.6. Возведение комплексных чисел в степень.
Формула Муавра
Начнем со всеми любимого квадрата:
Пример 9
Возвести в квадрат комплексное число 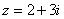
Решение: здесь можно пойти несколькими путями, первый способ это переписать степень как произведение множителей 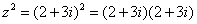 и перемножить числа по правилу умножения многочленов. и перемножить числа по правилу умножения многочленов.
Второй способ состоит в применение известной школьной формулы сокращенного умножения 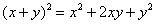 (см. Приложение Горячие формулы): (см. Приложение Горячие формулы):
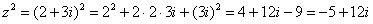
Для комплексного числа легко вывести свою формулу сокращенного умножения:
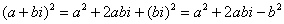 . Аналогичные формулы можно вывести для квадрата
разности, а также для куба сумма и куба разности. Но все они более актуальны в задачах комплексного анализа, поэтому сейчас я
воздержусь от подробных выкладок. . Аналогичные формулы можно вывести для квадрата
разности, а также для куба сумма и куба разности. Но все они более актуальны в задачах комплексного анализа, поэтому сейчас я
воздержусь от подробных выкладок.
Хорошо, с квадратом и кубом разобрались. Но что делать, если комплексное число нужно возвести, скажем, в 5-ю, 10-ю или 100-ю степень?
Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде 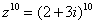 ? И это ещё только десять множителей. ? И это ещё только десять множителей.
И здесь на помощь приходит тригонометрическая форма комплексного числа. Но прежде я
познакомлю вас с обещанной формулой:
Чтобы перемножить два комплексных числа, представленных в тригонометрической форме 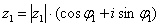 , , 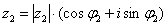 , нужно перемножить их модули, а аргументы
– сложить: , нужно перемножить их модули, а аргументы
– сложить:
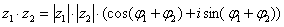
Но когда вам предложено вычислить 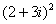 , так извращаться,
конечно, не надо J Зато этот способ невероятно эффективен при возведении числа в высокие степени: , так извращаться,
конечно, не надо J Зато этот способ невероятно эффективен при возведении числа в высокие степени:
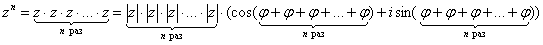
В результате получается так называемая, формула Муавра:
Если комплексное число 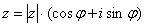 – представлено в тригонометрической форме, то при его возведении в натуральную
степень – представлено в тригонометрической форме, то при его возведении в натуральную
степень 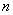 справедлива
формула справедлива
формула 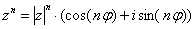
Аналогично для показательной формы: если 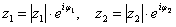 , то: , то:
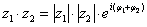 и формула Муавра принимает вид: и формула Муавра принимает вид: 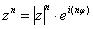
Просто до безобразия:
Пример 10
Дано комплексное число 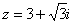 , найти , найти 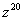 . .
Решение: сначала нужно представить данное число в тригонометрической
форме, что мы уже сделали в Примере 8:
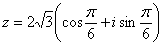
Тогда, по формуле Муавра:
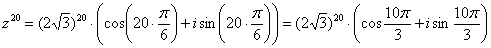
паси вас, не нужно считать на калькуляторе 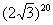 , а вот
угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет , а вот
угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет 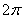 радиан или 360 градусов. Выясним сколько у нас
оборотов в аргументе радиан или 360 градусов. Выясним сколько у нас
оборотов в аргументе 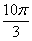 . Для удобства делаем дробь
правильной: . Для удобства делаем дробь
правильной: 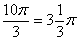 , после чего становится хорошо видно, что
можно убавить один оборот: , после чего становится хорошо видно, что
можно убавить один оборот: 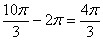 (надеюсь всем понятно,
что (надеюсь всем понятно,
что 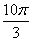 и и 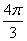 – это один и тот же угол). – это один и тот же угол).
Таким образом, окончательный ответ запишется так:
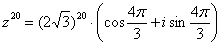
Любители стандартов везде и во всём могут переписать ответ в виде:
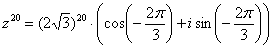 (т. е. убавить ещё один оборот и получить
значение аргумента в стандартном виде). (т. е. убавить ещё один оборот и получить
значение аргумента в стандартном виде).
Хотя, 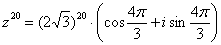 – это ни в коем случае не ошибка,
впрочем, всё зависит от блажи рецензента. – это ни в коем случае не ошибка,
впрочем, всё зависит от блажи рецензента.
Решаем самостоятельно:
Пример 11
Дано комплексное число 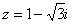 , найти , найти 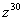 . Полученный аргумент (угол) упростить, результат представить в
алгебраической форме. . Полученный аргумент (угол) упростить, результат представить в
алгебраической форме.
Полное решение и ответ в конце книги.
Отдельный жанр – это возведение в степень чисто мнимых чисел:
Пример 12
Возвести в степень комплексные числа 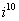 , , 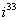 , , 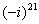
Решение: здесь тоже всё просто, главное, помнить знаменитый факт 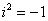 . .
Если мнимая единица возводится в чётную степень, то техника решения такова:
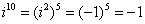
Если мнимая единица возводится в нечётную степень, то сначала «отщипываем» одно «и», получая четную степень:
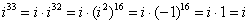
Если есть «минус» (или любой действительный коэффициент), то его удобно предварительно отделить:
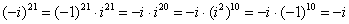
Пример 13
Возвести в степень комплексные числа 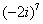 , , 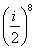
Это пример для самостоятельного решения.
 2.1.7. Извлечение корней из комплексных чисел 2.1.7. Извлечение корней из комплексных чисел
 2.1.5. Показательная форма комплексного числа 2.1.5. Показательная форма комплексного числа
| Оглавление |
|