|
Ваш репетитор, справочник и друг!
|
2.1.7. Извлечение корней из комплексных чиселНаконец-то. Меня всю дорогу «подмывало» привести этот маленький примерчик: …Нельзя извлечь корень? Если речь идет о действительных числах, то действительно нельзя. Но в комплексных числах извлечь корень можно! Точнее, два корня:
Часто используется сокращенная запись, оба корня записывают в одну строчку под «одной гребёнкой»: Действительно ли найденные корни являются решением уравнения Что и требовалось проверить. Как извлекать квадратные корни из отрицательных действительных чисел, думаю, всем понятно: Как извлечь квадратный корень из комплексного числа с ненулевой мнимой частью, мы узнаем совсем скоро, но сначала нечто знакомое: Пример 14 Решить квадратное уравнение Решение проведём по известным формулам (см. Приложение Горячие формулы). Вычислим дискриминант: Дискриминант отрицателен, и в действительных числах уравнение решения не имеет. Но корень можно извлечь в комплексных числах! В результате получаем: Таким образом, уравнение Нетрудно понять, что в поле комплексных чисел «школьное» квадратное уравнение всегда имеет два корня! И не за горами глава, где мы здОрово разовьём эту тему. Простенький пример для самостоятельного решения: Пример 15 Найти корни уравнения Разложение на множители осуществляется опять же по стандартной «школьной» формуле (см. Приложение Горячие формулы). Как извлечь корень из произвольного комплексного числа? Рассмотрим уравнение вида
Уравнение вида Сначала для разминочки квадрат: Пример 16 Найти корни уравнения Решение: перепишем уравнение в виде Найдём модуль и аргумент комплексного числа Число Для самоконтроля можно изобразить число Теперь ещё более детализируем формулу:
На чистовик так подробно оформлять, конечно, не нужно, это сделано мной для того, чтобы вам было понятно, откуда что взялось. Подставляя в формулу значение Подставляя в формулу значение Ответ: При желании или требовании задания, полученные корни нетрудно перевести обратно в алгебраическую форму, тем более, здесь получились «хорошие» аргументы, который есть в Таблице значений тригонометрических функций (см. Приложение Тригонометрические таблицы). Рассмотрим более содержательное задание: Пример 17 Найти корни уравнения Решение: сначала представим уравнение в виде Для разрешения уравнения относительно «зет» извлечём корень 3-й степени из обеих частей, в результате чего задача сведётся к
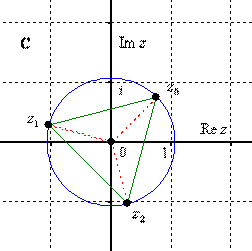
извлечению корня В данном примере Детализирую общую формулу: Найдем модуль и аргумент комплексного числа Число Ещё раз детализирую формулу, сразу упрощая корень Подставляем в формулу значение Подставляем в формулу значение Подставляем в формулу значение Часто полученные корни требуется изобразить графически. Как выполнить чертеж? Сначала на калькуляторе находим, чему равен модуль корней Теперь берём аргумент первого
корня Берём аргумент второго корня И по такому же алгоритму строится точка Легко заметить, что корни расположены геометрически правильно с интервалом Чертеж крайне желательно выполнять с помощью транспортира. Если вы отмерите углы «на глазок», то рецензент, скорее всего, это заметит и с высокой вероятностью поставит «минус» за чертеж. Следующее задание для самостоятельного решения Пример 18 Вычислить Сверяемся с образцом и переходим к насыщенному практикуму по теме:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих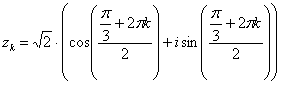 ,
, 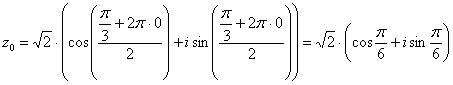
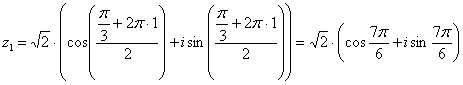
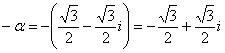 . Переобозначим «минус альфа» формульной
буквой:
. Переобозначим «минус альфа» формульной
буквой: 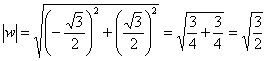
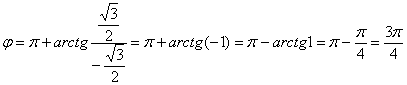
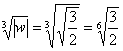 :
: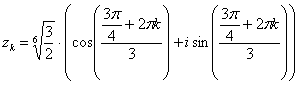 ,
, 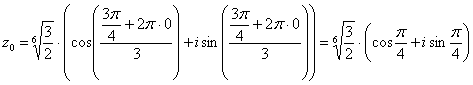
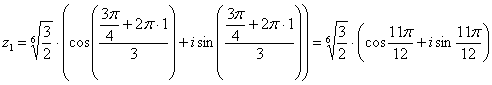
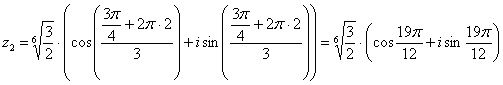
 2.2. Выражения с комплексными числами
2.2. Выражения с комплексными числами 2.1.6. Возведение комплексных чисел в степень. Формула Муавра
2.1.6. Возведение комплексных чисел в степень. Формула Муавра