Ваш репетитор, справочник и друг!

Высшая алгебра для начинающих

3.4. Корни многочлена

Рассмотрим полином степени с комплексными коэффициентами (в частности, они могут быть действительными, рациональными, целыми или даже натуральными).

Комплексное число («цэ») называют корнем многочлена, если оно является корнем уравнения . Иными словами, при подстановке этого значения в многочлен получается ноль:
.

Неоправданно «громкое» название, но так оно сложилось:

основная теорема алгебры: всякий многочлен (см. выше), отличный от константы, имеет по крайне мере один корень, в общем случае комплексный.

И практически более важное следствие основной теоремы алгебры: многочлен имеет ровно комплексных корней.

Если некоторое комплексное число является корнем многочлена, то и сопряжённое ему число – тоже обязательно корень этого многочлена (напоминаю, что сопряжённые комплексные числа имеют вид ). Это, к слову, ещё одно из следствий.

Некоторые корни многочлена (или даже все) могут быть в частности действительными. При этом среди действительных корней могут встретиться кратные (одинаковые) корни (минимум два, максимум штук).

На практике чаще всего встречаются многочлены с действительными, более того, целыми коэффициентами , и для них, естественно, все эти выкладки в силе. Далее, если не сказано иного, имеем в виду действительные коэффициенты.

Так, многочлен 1-й степени имеет один действительный корень. Чтобы его найти нужно решить элементарное линейное уравнение:

Найдём, например, корень многочлена . Для этого решим соответствующее линейное уравнение: . И в самом деле, при подстановке этого значения в многочлен: – получается ноль.

Многочлен 2-й степени имеет ровно два корня. Квадратное уравнение мы уже исследовали вдоль и поперёк и выяснили, что оно имеет либо два действительных корня (различных или кратных), либо два сопряжённых комплексных корня.

В простейшем случае , кстати, получаются кратные корни , ну и популярнейший школьный вариант а-ля – это различные действительные корни: . Если же корни комплексные, то они непременно сопряжены по отношению друг к другу, согласно утверждению выше.

Полином 3-й степени имеет ровно три корня, при этом хотя бы один из них – действительный. Последний факт, к слову, справедлив для любого многочлена нечётной степени с действительными коэффициентами.

Простейший экземпляр обладает тремя кратными корнями .

И есть частные случаи, с решением которых нет проблем – это когда свободный член . В таких примерах просто выносим «икс» либо «икс квадрат» за скобку, например:
– уравнение – имеет один действительный корень и сопряжённые комплексные корни (решение изящного уравнения мы разобрали здесь).

Более трудная ситуация, это когда ВСЕ коэффициенты многочлена не равны нулю (полегче будет при ). Но существуют формулы Кардано, которые позволяют найти , в том числе выразить иррациональные корни точно, если таковые есть.

Для многочлена 4-й степени тоже существует аналитический метод нахождения корней (метод Феррари), но в простых частных случаях он ни к чему. Так, если , то опять выполняем вынесение за скобки ( или ). Особой и важной разновидностью является многочлен вида . Чтобы найти его корни нужно решить биквадратное уравнение:

Оно сводится к квадратному уравнению путём замены :

Пример 37

Найти корни многочлена

Решение: решим биквадратное уравнение:

Проведём замену :

Вычислим дискриминант (Приложение Горячие формулы, кто не запомнил формулы) и корень из него:

Находим корни и вспоминаем, что :
, откуда получаем первую пару корней: , и:

Ответ:

В этом примере получились действительные корни, но очевидно, биквадратное уравнение может иметь пару или даже две сопряжённых комплексных корней.

Если для многочленов 3-й и 4-й степени всё ещё существуют формулы нахождения корней, то для старших собратьев ситуация куда более грустная. Зачастую корни приходится подбирать вручную, и мы познакомимся как раз с этим алгоритмом. Дело в том, что во многих темах вышмата нахождение корней – это всего лишь вспомогательная задача. Именно поэтому в рамках этой книги я не разобрал громоздкие формулы Кардано и кропотливый алгоритм Феррари. Как говорится, Гугл в помощь, ничего сложного там нет.

Самостоятельно решаем более актуальные примеры:

Пример 38

Найти корни следующих многочленов:

сверяемся и продолжаем:

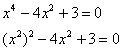
3.4.1. Как найти рациональные корни многочлена?

3.3. Деление многочленов

| Оглавление |

Автор: Aлeксaндр Eмeлин