3.4.1. Как найти рациональные корни многочлена?
В большинстве задач, как вы уже заметили, нам встречаются многочлены с целыми коэффициентами. И очень
часто нужно узнать, есть ли у такого многочлена рациональные, в частности целые корни?
Вот у многочлена 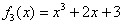 – есть они или нет? Свободный член
здесь не равен нулю, и отделаться «малой кровью», как в предыдущих примераx, вряд ли получится. Но мы попробуем. И первое, что приходит в
голову – это метод научного, а точнее, практического тыка :) Метод подбора наудачу. – есть они или нет? Свободный член
здесь не равен нулю, и отделаться «малой кровью», как в предыдущих примераx, вряд ли получится. Но мы попробуем. И первое, что приходит в
голову – это метод научного, а точнее, практического тыка :) Метод подбора наудачу.
Просто начинаем подставлять в уравнение 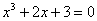 различные целые числа, претендующие на звание «корень». Прежде всего, напрашивается подстановка единичных значений. Подставим различные целые числа, претендующие на звание «корень». Прежде всего, напрашивается подстановка единичных значений. Подставим 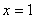 : :
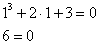
Получено неверное числовое равенство, таким образом, единица «не подошла». Ну да ладно, подставляем 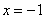 : :
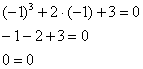
Получено верное равенство! Таким образом, значение 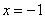 является корнем данного уравнения и соответствующего многочлена. является корнем данного уравнения и соответствующего многочлена.
Но возникает вопрос: а нет ли подобных корней ещё? Как быть?
Использовать следствие теоремы Безу. Да, сначала приведу следствие: число 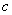 является корнем многочлена тогда и только тогда, когда многочлен является корнем многочлена тогда и только тогда, когда многочлен 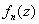 делится на двучлен делится на двучлен 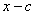 без остатка. При этом получается многочлен
степенью ниже: без остатка. При этом получается многочлен
степенью ниже: 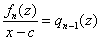 . .
И переписав сей факт в виде 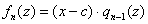 , выясняется очень крутая
вещь: если мы нашли какой-либо корень многочлена , выясняется очень крутая
вещь: если мы нашли какой-либо корень многочлена 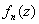 , то можем
выполнить деление, найти более простой многочлен , то можем
выполнить деление, найти более простой многочлен 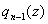 и из
уравнения и из
уравнения 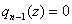 вытряхивать другие корни! вытряхивать другие корни!
В нашем скромном примере 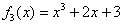 был подобран корень был подобран корень 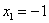 , а значит, при делении , а значит, при делении 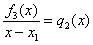 – получится многочлен второй степени. Представив исходный многочлен в виде – получится многочлен второй степени. Представив исходный многочлен в виде 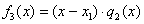 , становится ясно, что остальные корни многочлена , становится ясно, что остальные корни многочлена 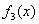 элементарно достаются из квадратного уравнения элементарно достаются из квадратного уравнения 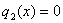 . Найдём соответствующий многочлен, делим «столбиком»: . Найдём соответствующий многочлен, делим «столбиком»:
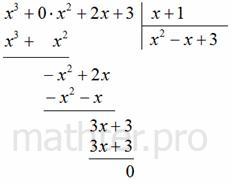
Таким образом, 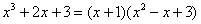 и осталось разобраться с квадратным
уравнением и осталось разобраться с квадратным
уравнением 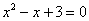 . Вычислим дискриминант: . Вычислим дискриминант: 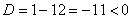 , и коль скоро он таков, то получаются сопряжённые комплексные корни: , и коль скоро он таков, то получаются сопряжённые комплексные корни: 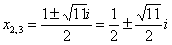 . .
В результате все корни многочлена найдены: 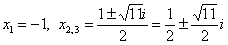 . .
Но чаще, повторюсь, нас будут интересовать корни рациональные, целые. И для таких корней метод подбора действительно заманчив. Но процесс
может затянуться:
1, –1, 2, –2, 3, –3, … (порядок перебора обычно таков)
…А может быть какие-то значения из этого списка и рассматривать-то смысла нет? А может корень дробный? – элементарно 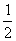 , а мы тут сидим, паримся с целыми числами. А что, если рациональных
корней нет вообще? , а мы тут сидим, паримся с целыми числами. А что, если рациональных
корней нет вообще?
К счастью, существует теорема (и не одна), которая позволяет значительно сократить перебор значений-«кандидатов» в рациональные корни.
Теорема: рассмотрим несократимую дробь 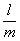 , где , где 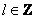 , а , а 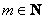 . Если число . Если число 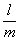 является корнем многочлена является корнем многочлена 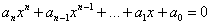 с целыми (!) коэффициентами с целыми (!) коэффициентами 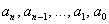 , то свободный член , то свободный член 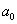 делится на делится на 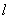 , а
старший коэффициент , а
старший коэффициент 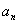 – на – на 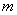 . .
Заметьте, что теорема не гарантирует наличие рационального корня (естественно), но уж если он есть: 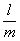 (дробь несократима!!), то свободный член (дробь несократима!!), то свободный член 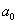 обязательно делится на обязательно делится на 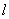 , а старший коэффициент , а старший коэффициент 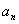 – на – на 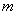 . В
частности, при . В
частности, при 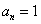 знаменатель дроби знаменатель дроби 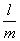 равен единице. Таким образом, рациональные корни такого
многочлена (если они существуют) могут быть только целыми: равен единице. Таким образом, рациональные корни такого
многочлена (если они существуют) могут быть только целыми: 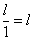 . .
И мы начинаем эксплуатировать теорему как раз с этой вкусной частности. Вернёмся к многочлену 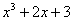 . Так как его старший коэффициент . Так как его старший коэффициент 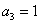 , то гипотетические рациональные корни могут быть исключительно
целыми, причём свободный член должен обязательно делиться на эти корни без остатка. А «тройку» можно разделить только на 1, –1, 3 и
–3. То есть у нас всего лишь 4 «кандидата» в корни. И, согласно Теореме, другие рациональные числа не могут быть
корнями этого уравнения В ПРИНЦИПЕ. , то гипотетические рациональные корни могут быть исключительно
целыми, причём свободный член должен обязательно делиться на эти корни без остатка. А «тройку» можно разделить только на 1, –1, 3 и
–3. То есть у нас всего лишь 4 «кандидата» в корни. И, согласно Теореме, другие рациональные числа не могут быть
корнями этого уравнения В ПРИНЦИПЕ.
Подбор корней чаще всего проводят «цивилизованным» способом:
 3.4.2. Схема Горнера 3.4.2. Схема Горнера
 3.4. Корни многочлена 3.4. Корни многочлена
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих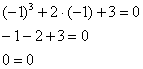
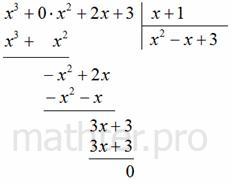
 3.4.2. Схема Горнера
3.4.2. Схема Горнера 3.4. Корни многочлена
3.4. Корни многочлена