Ваш репетитор, справочник и друг!

Высшая алгебра для начинающих

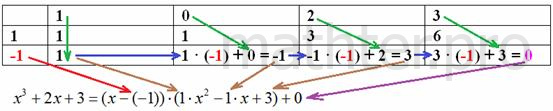
3.4.2. Схема Горнера

По существу, это деление «столбиком» многочлена на двучлен (!) с более чётким (на мой взгляд) алгоритмом и оформлением решения. И в общем случае, конечно, речь идёт о деление с остатком.

Теорема Безу: остаток при делении многочлена на двучлен в точности равен – значению этого многочлена в точке «а»: .
В частности, если – корень многочлена, то этот остаток нулевой , что фактически уже было озвучено выше (следствие теоремы Безу).

Итак, мы только что выяснили, что если у многочлена и есть рациональные корни, то они находятся в списке 1, –1, 3, –3. Начинаем проверять «кандидатов» с помощью схемы Горнера:

Сначала запишем исходный многочлен со всеми, в том числе нулевыми коэффициентами: , после чего занесём эти коэффициенты (строго по порядку) в верхнюю строку таблицы:

Проверку начнём с наиболее простого значения , записываем его слева:

Сносим сверху старший коэффициент многочлена:

Процесс заполнения нижних ячеек чем-то напоминает шитьё, где красная единица – это своеобразная «игла», пронизывающая следующие шаги. Снесённый коэффициент умножаем на 1 (синяя стрелка) и прибавляем к произведению число из верхней ячейки:

Найденное значение переносим направо (синяя стрелка), умножаем на «красную иглу» и к произведению прибавляем следующий коэффициент уравнения:

И, наконец, полученное значение снова переносим направо (синяя стрелка) и «обрабатываем иглой», после чего добавляем коэффициент сверху:

В результате многочлен представлен в виде , а именно:

Таким образом, мы разделили многочлен на двучлен – с частным и остатком 6. Проверим, что остаток – это действительно значение исходного многочлена в «красной» точке: , в чём и хотелось убедиться. Ну и для пущей уверенности – раскройте скобки правой части и приведите подобные слагаемые, в результате получится левая часть, …устно!

Так как остаток не равен нулю , то проверенное значение не является корнем многочлена , и в списке возможных корней осталось три «кандидата»: –1, 3, –3.

«Прогоним» по схеме Горнера значение . При этом удобно использовать ту же таблицу – записываем слева новую «иглу», сносим сверху старший коэффициент (левая зелёная стрелка), и понеслось:

И ноль в правой нижней ячейке говорит нам о том, что многочлен разделился на без остатка. И в самом деле: .
Таким образом, является корнем многочлена . Кроме того, мы представили его в виде , получив возможность легко вытряхнуть оставшиеся корни из квадратного уравнения , что уже сделано ранее.

Аналогичное задание для самостоятельного решения:

Пример 39

С помощью схемы Горнера найти рациональные корни многочлена , …они такие хорошие, такие пушистые, что их прямо так и хочется найти! :)

Не забываем предварительно определить список возможных корней, после чего последовательно «заряжаем» их по схеме Горнера. Обратите внимание, что числа 1 и –1 являются «завсегдатаями» списка (прямое следствие теоремы) и самым лучшим выбором для первоочередной проверки. Сверяем и переходим к более содержательным задачам:

Пример 40

Найти рациональные корни многочлена

Решение: поскольку старший коэффициент , то гипотетические рациональные корни могут быть только целыми, при этом они обязательно должны быть делителями свободного члена. «Минус» сОрок делится на следующие пары чисел:
– итого 16 «кандидатов» в корни.

И здесь сразу появляется заманчивая мысль: а нельзя ли отсеять все отрицательные или все положительные корни? В ряде случаев можно! Сформулирую два признака:

1) Если все коэффициенты многочлена неотрицательны или все неположительны, то он не может иметь положительных корней. К сожалению, это не наш случай. Вот если бы нам был дан полином – тогда да, при подстановке любого его значение строго положительно , а значит, все положительные числа (причём, и иррациональные тоже) не могут быть корнями уравнения .

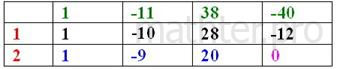
2) Если коэффициенты при всех нечётных степенях неотрицательны, а при всех чётных степенях (включая свободный член) – отрицательны, то многочлен не может иметь отрицательных корней. Или «зеркально»: если коэффициенты при всех нечётных степенях неположительны, и при всех чётных – положительны.
Это наш случай! Немного присмотревшись, можно заметить, что при подстановке в многочлен любого отрицательного «икс» он будет строго отрицателен , а значит, отрицательные корни (в том числе иррациональные) отпадают.

Таким образом, для исследования осталось 8 чисел:

Последовательно «заряжаем» их по схеме Горнера. Надеюсь, вы уже освоили устные вычисления:

Удача поджидала нас при тестировании «двойки». Таким образом – есть корень многочлена, и коэффициенты разложения легко снимаются из нижней строки:
.

Осталось исследовать уравнение . Это легко сделать через дискриминант, но я проведу показательную проверку по той же схеме. Во-первых, обратим внимание, что свободный член равен 20, а значит, по Теореме, из списка возможных корней выпадают числа 8 и 40 (т. к. 20 не делится на них), и для исследования остаются значения (единица отсеялась на первом шаге).

Записываем коэффициенты трёхчлена в верхнюю строку новой таблицы и начинаем проверку с той же «двойки». Почему? А потому что корни могут быть и кратны, пожалуйста: – это уравнение имеет 10 одинаковых корней. Но не отвлекаемся:

и здесь я, конечно, знал, что корни рациональны. Ведь если они были бы иррациональными или комплексными, то мне светила бы безуспешная проверка всех оставшихся чисел. Поэтому на практике руководствуйтесь дискриминантом.

Ответ: рациональные корни: 2, 4, 5

Более интересная задачка для самостоятельного решения:

Пример 41

Найти рациональные корни многочлена

Особенность состоит в том, что после нахождении первого рационального корня (если он существует) получится многочлен 3-й степени , для которого вновь нужно определить список возможных корней, причём, этот список следует скорректировать – его значения должны обязательно входить и в первоначальный список.

В представленных примерах у нас получался не слишком большой список возможных корней, но на практике бывает гораздо хуже. И для таких случаев существует ещё одна теорема, позволяющая сокращать список по ходу решения. Желающие и нуждающиеся могут ознакомиться с этим, более редким материалом в соответствующей статье сайта. Ну а мы рассмотрим ещё один достаточно важный приём:

3.4.3. Как определить корни графически?

3.4.1. Как найти рациональные корни многочлена?

| Оглавление |