|
Ваш репетитор, справочник и друг!
|
3.4.3. Как определить корни многочлена графически?В некоторых ситуациях бывает удобно использовать графический метод нахождения рациональных корней. Более того, есть задачи, где нужно выяснить – а имеет ли многочлен / уравнение хоть какие-то действительные корни? И если да, то примерно где находятся эти корни – на каких промежутках? Сначала наш подопытный многочлен: Пример 42 Определить количество действительных корней Решение: задачу сведём к
графическому решению уравнения Запишем уравнение в виде Ответ: один Как вариант, можно было рассмотреть уравнение К слову, многочлен Пример 43 Графическим методом определить количество действительных корней многочлена и указать единичные отрезки, на которых расположены эти
корни: Следует заметить, что графический метод удачно срабатывает как раз в таких случаях – когда есть старший член + младший двучлен для
построения прямой. И коль скоро место осталось на странице, то само провИдение за то, чтобы я всё-таки рассказал о графиках! Сейчас только
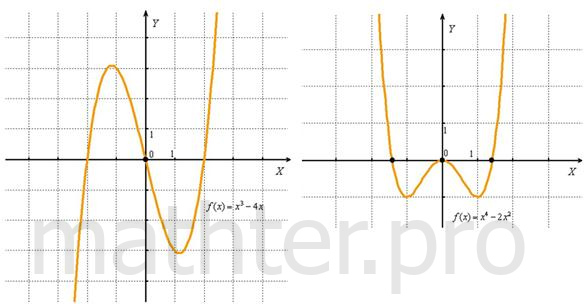
скопирую откуда-нибудь пару чертежей…: Типичный график функции-многочлена нечётной степени имеет вид «молнии» (чертёж слева). Принципиально так же выглядят графики 5, 7, 9 и т. д. степеней, только «загогулин» там будет больше, в зависимости от степени. И здесь мы наглядно убедились в том, что многочлен нечётной степени имеет хотя бы один действительный корень. График функции-многочлена чётной степени принципиально имеет вид параболы, чаще всего с промежуточными извилинами (чертёж
справа), количество которых опять же зависит от степени. Многочлен чётной степени может и не иметь действительных корней – в тех
случаях, когда «парабола» полностью лежит выше или ниже оси Вот, пожалуй, и вся практически важная информация о многочленах. Желающие могут ознакомиться с богатой теорией и дополнительной практикой этого раздела алгебры в сторонних источниках. |
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих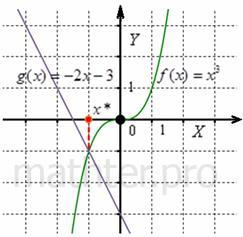
 4. Матрицы и определители
4. Матрицы и определители 3.4.2. Схема Горнера
3.4.2. Схема Горнера