Ваш репетитор, справочник и друг!

Высшая алгебра для начинающих

3.3. Деление многочленов

Важное и невероятно полезное действие, которое встретится вам в самых разных разделах математики. Сначала повторим терминологию, потренируемся на ~~кошках~~ числах:

Число, которое делят (350) называется делимое. Число НА которое делят (7), называется делитель. Полученное в результате деления число (50) называют частное.

В этом примере 350 на 7 разделилось нацело, но чаще, конечно, встречается деление с остатком: . Число 61 называют неполным частным, а число 5 (да, именно пять) – остатком от деления 432 на 7. Такое деление называют целочисленным, при этом остаток (5) строго меньше делителя (7), то есть остаточная дробь – правильная.

У многочленов всё аналогично! Используем тот же принцип и термины:

Для краткости степень верхнего многочлена будем называть степенью числителя, а степень нижнего многочлена – степенью знаменателя. Многочлен будем называть просто частным и полагать, что он ненулевой: .

Деление осуществимо, если исходная дробь неправильная, то есть степень числителя больше либо равна степени знаменателя: , и, разумеется, нижний многочлен должен быть ненулевым: . Многочлен является остатком от деления и его степень строго меньше , то есть остаточная дробь – правильная. В самом вкусном случае остаток нулевой.

Как разделить многочлен на многочлен? В простых или достаточно простых случаях удобен метод искусственного преобразования числителя:

Пример 30

Выполнить деление:

Решение: в первом случае деление не проходит, так как дробь – правильная (степень числителя строго меньше степени знаменателя).

Смотрим на вторую дробь: – она неправильная (степень числителя равна степени знаменателя), а значит, деление осуществимо. Проще всего преобразовать числитель, а именно организовать там . Для этого прибавляем наверху двойку, и чтобы ничего не изменилось – тут же её вычитаем:

после чего, выполняем нужное почленное деление, распишу очень подробно:
, готово.

Проверка элементарна, приведём полученное выражение к общему знаменателю:
– в результате получена исходная дробь.

В третьем случае деление тоже осуществимо, по той же схеме:

Представленные примеры настолько простЫ, что даже неловко предлагать аналогичные для самостоятельного решения. Рассмотрим более содержательное задание:

Пример 31

Выполнить деление:

Решение: рассуждаем примерно так:

1) В числителе нам нужно организовать , но там . Что делать? Заключаем в скобки и умножаем на «икс»: .

2) Теперь раскрываем эти скобки, что получается? . …Хммм, но никакой двойки при изначально в числителе нет. Поэтому домножаем нашу «заготовку» на :

3) И снова раскрываем скобки: . А вот и первый успех! Нужный получился! Но проблема в том, что появилось лишнее слагаемое . Что делать? Чтобы выражение не изменилось, мы обязаны прибавить к нашей конструкции :
, жить стало легче, жить стало веселее.

А нельзя ли ещё раз в числителе организовать ?

4) Можно! Пробуем: . Раскрываем скобки второго слагаемого:
. Простите, но у нас вообще-то было на предыдущем шаге , а не . Что делать? Нужно домножить второе слагаемое на :

5) И снова для проверки раскрываем скобки во втором слагаемом:
– вот теперь нормально: получено из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое , значит, мы обязаны прибавить ко всему выражению :

Если всё выполнено правильно, то при раскрытии всех скобок у нас должен получиться исходный числитель. Проверяем:
Отлично!

Теперь осталось поместить взращенного монстра в числитель и АККУРАТНО выполнить почленное деление:

Для пущей уверенности выполним контрольную проверку, приведём дроби к общему знаменателю:

В результате получена исходная дробь, что мы и хотели увидеть.

Следующий пример для самостоятельного решения:

Пример 32

Разделить

Подбор числителя и промежуточные проверки обычно проводят на черновике либо устно (кто приноровился). Краткое решение в конце книги.

В более трудных случаях многочлены обычно делят «столбиком». Как обычные числа. Но чтобы не разводить путаницу, я не буду вспоминать «школьный» алгоритм деления, лучше сразу возьмём многочлены за члены и разделим «столбиком» только что разобранную дробь . Во-первых, у исходных многочленов нужно прописать ВСЕ нулевые члены (если таковые есть), оформляем «заготовку» для деления:

Подбираем ТАКОЙ одночлен, чтобы при его умножении на получился . Записываем этот одночлен справа внизу:

И в самом деле, при умножении – получен старший одночлен делимого.

Теперь умножаем на делитель, то бишь на и на , результат пишем слева:

Проводим отчёркивание и из вычитаем :

Распишу почленно: (ноль не пишем), .

Сносим сверху (из делимого) ноль:

И алгоритм заходит «на второй круг». Подбираем ТАКОЙ одночлен, чтобы при его умножении на получилось . Приплюсовываем этот одночлен справа под чертой:

И в самом деле: . Умножаем одночлен на и на , отчёркиваем и вычитаем из полученный результат :

Зелёным кружком я обвёл частное , а красным – остаток от деления , и в соответствии с формулой:

Рассмотрим случай посолиднее:

Пример 33

Разделить

Решение: совершенно понятно, что эта дробь неправильная, а значит, деление осуществимо. Сначала рисуем «заготовку» для деления «столбиком», при этом внимательно прописываем недостающие нулевые члены, они тут есть и в числителе и в знаменателе:

И та же задачка: какой одночлен нужно умножить , чтобы получить ? Очевидно, что это :

Теперь умножаем на делитель: сначала на , затем на , затем на , и, наконец, на 0. Записываем результаты слева:

Отчёркиваем и производим почленное вычитание (из верха вычитаем низ), к результату сносим из делимого свободный член :

Старшая степень полученного многочлена равна двум, а старшая степень делителя – больше, она равна трём, поэтому больше разделить не удастся. Таким образом, – частное, а – остаток от деления.

И в соответствии с формулой :
ответ:

Этот пример легко решить искусственным преобразованием числителя, благо, шаг здесь всего лишь один, повезло, что с «кубами» всё сложилось удачно:

Следующий пример для самостоятельного решения, маньячить сильно не будем:

Пример 34

Разделить , выполнить проверку

На практике особо часто встречается деление многочлена не двучлен 1-й степени, и чтобы окончательно закрепить алгоритм деления добавим формул и красок:

Пример 35

Разделить

Решение: записываем начальный шаблон для деления «столбиком», не забывая при этом про недостающее нулевое слагаемое:

Теперь в углу нужно разоблачить незнакомца :

Каким он должен быть? Девчонки, признавайтесь! …Нет-нет-нет, он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :

Решаем это простенькое уравнение и получаем:

Действительно, . Записываем первый трофей:

Теперь нашего героя нужно умножить на делитель: , а результат записать во второй строке слева:

Отчёркиваем и проводим почленное вычитание: (ноль под чертой не пишем) и :

Сносим сверху следующее слагаемое:

и алгоритм идёт на следующий круг. Снова ищем одночлен , он должен быть ТАКИМ, чтобы при его умножении на «икс» получилось :

Решаем уравнение и добавляем корень справа под чертой:

Умножаем на делитель: – записываем это 4-й строкой:

Ещё раз отчёркиваем и проводим почленное вычитание: (ноль под чертой не пишем) и :

Сносим сверху (из делителя) последнее слагаемое:

И организуем завершающий цикл. Необходимо подобрать третье слагаемое , которое при умножении на «икс» даёт :

Находим корень уравнения: и добавляем его на законное место:

Умножаем на делитель: – записываем итог в 6-ю строку:

Выполняем завершающее отчёркивание и почленное вычитание:

Таким образом, частное , остаток , то есть многочлены у нас разделились «нацело» – без остатка: . Это особый случай, который мы разберём скоро, но сначала не ленимся:

Пример 36

Разделить и выполнить проверку ;)

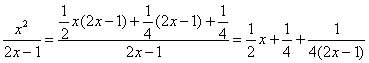
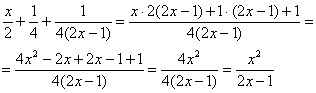
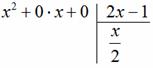
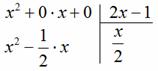
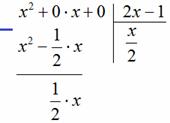
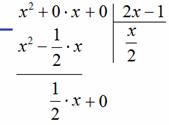
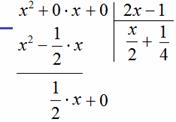
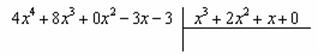
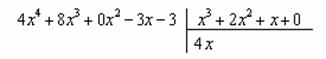
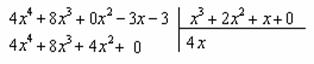
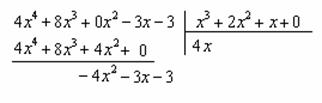
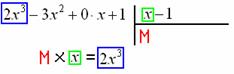
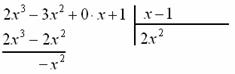
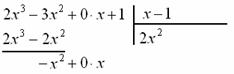
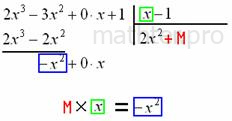
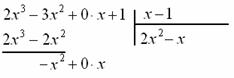
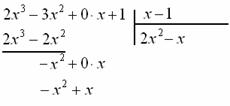
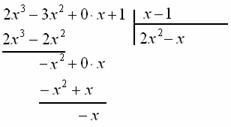
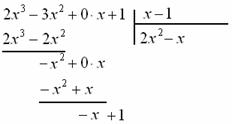
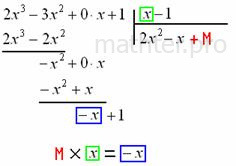
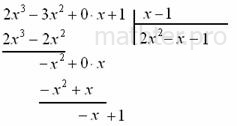
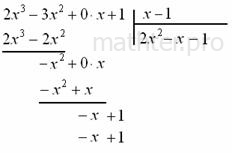
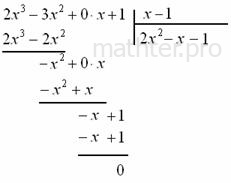
3.4. Корни многочлена

3.2. Кольцо многочленов

| Оглавление |

Автор: Aлeксaндр Eмeлин