3.2. Кольцо многочленов
Небольшой теоретический параграф, который будет полезен всем – мало ли кто не знает, какие ещё есть «фишки» у многочленов….
Рассмотрим 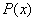 – множество многочленов одной переменной с действительными (например) коэффициентами.
Напоминаю, что также можно рассмотреть либо целые, либо рациональные, либо комплексные коэффициенты. В данном случае это не принципиально. – множество многочленов одной переменной с действительными (например) коэффициентами.
Напоминаю, что также можно рассмотреть либо целые, либо рациональные, либо комплексные коэффициенты. В данном случае это не принципиально.
С точки зрения алгебраической структуры, множество 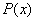 с определёнными на нём операциями сложения и умножения представляет собой кольцо. с определёнными на нём операциями сложения и умножения представляет собой кольцо.
Доказательство этого утверждения состоит в проверке аксиом кольца. Дабы не городить страшные записи с кучей букв и индексов я
подробно обосную лишь одну аксиому, удобно начать с четвёртой:
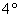 Для любых многочленов Для любых многочленов 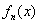 (степень (степень 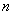 ) и ) и 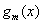 (степень (степень 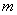 ),
принадлежащих множеству ),
принадлежащих множеству 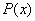 , справедливо свойство коммутативности: , справедливо свойство коммутативности:
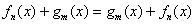
Повторюсь, что это хоть и кажется «элементарщиной», но выполнено далеко не для всех алгебраических объектов. А посему в суровой алгебре
даже такие «очевидные» факты подлежат проверке: для определённости положим, что степень первого многочлена больше степени
второго: 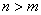 . Тогда многочлены можно расписать следующим
образом: . Тогда многочлены можно расписать следующим
образом:
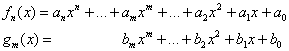
Чтобы сложить многочлены, нужно сложить их коэффициенты при соответствующих степенях:
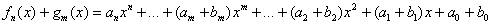
Теперь сложим многочлены в другом порядке:
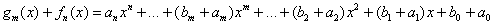
Для действительных чисел имеет место коммутативность сложения, поэтому:
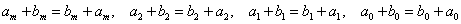
Таким образом, мы получили одинаковые многочлены (многочлены равны, если равны их соответствующие коэффициенты).
Свойство 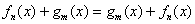 доказано. доказано.
И остальные аксиомы в обзорном порядке. Для всех многочленов множества 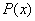 справедливо: справедливо:
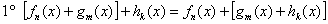 – свойство ассоциативности сложения. …Впервые тут
вроде встретились квадратные скобки, прокомментирую: в алгебраических выражениях квадратные скобки отличаются от круглых лишь своей
квадратностью :) Они используются для того, чтобы чётче были видны арифметические действия. – свойство ассоциативности сложения. …Впервые тут
вроде встретились квадратные скобки, прокомментирую: в алгебраических выражениях квадратные скобки отличаются от круглых лишь своей
квадратностью :) Они используются для того, чтобы чётче были видны арифметические действия.
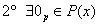 – во множестве многочленов существует нейтральный
элемент относительно сложения, это нулевой многочлен, степень которого не определена: – во множестве многочленов существует нейтральный
элемент относительно сложения, это нулевой многочлен, степень которого не определена:
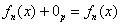 , и в самом деле, если к произвольному многочлену , и в самом деле, если к произвольному многочлену 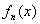 добавить нулевой многочлен добавить нулевой многочлен 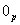 (сумму любого количества нулевых одночленов), то получится тот же самый многочлен (сумму любого количества нулевых одночленов), то получится тот же самый многочлен 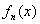 . .
Заметьте, что коль скоро я уже доказал 4-ю аксиому, то мне не нужно расписывать 2-ю аксиому в «классическом» виде 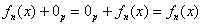 . .
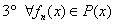 - для любого многочлена - для любого многочлена 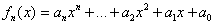 , принадлежащего множеству , принадлежащего множеству 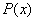 (проговариваем вслух!), (проговариваем вслух!), 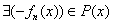 – существует противоположный многочлен, принадлежащий этому множеству, такой, что: – существует противоположный многочлен, принадлежащий этому множеству, такой, что:
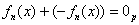
Это многочлен с противоположными коэффициентами:
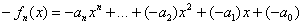
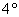 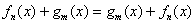 – доказана выше. – доказана выше.
Таким образом, 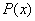 – это коммутативная группа относительно сложения. Но группой дело не ограничивается: – это коммутативная группа относительно сложения. Но группой дело не ограничивается:
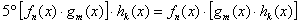 – ассоциативность умножения, то есть если вам дано
произведение трёх многочленов, например: – ассоциативность умножения, то есть если вам дано
произведение трёх многочленов, например: 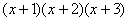 , то перемножать их
можно в любом порядке – сначала первые две скобки либо сначала две последние. И вполне хорошо, к слову, здесь работает устный алгоритм умножения. , то перемножать их
можно в любом порядке – сначала первые две скобки либо сначала две последние. И вполне хорошо, к слову, здесь работает устный алгоритм умножения.
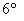 Свойства дистрибутивности (раскрытие скобок), справа: Свойства дистрибутивности (раскрытие скобок), справа:
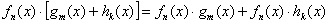
и слева:
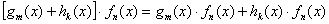
Этим свойством мы тоже фактически пользовались. Оно позволяет представить произведение по своему вкусу либо потребностям, например:
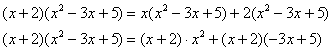
и тому подобное.
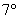 Во множестве Во множестве 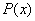 существует нейтральный относительно умножения элемент, это «единичный» многочлен существует нейтральный относительно умножения элемент, это «единичный» многочлен 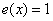 . Очевидно, что . Очевидно, что
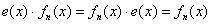
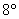 И, наконец, коммутативность умножения: И, наконец, коммутативность умножения:
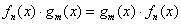 , а посему смело переставляйте множители, как вам удобно: , а посему смело переставляйте множители, как вам удобно: 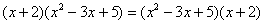 . .
Таким образом, 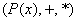 – это коммутативное
кольцо с единицей. Кольцо, но не поле, поскольку в общем случае аксиома – это коммутативное
кольцо с единицей. Кольцо, но не поле, поскольку в общем случае аксиома 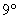 оказывается неверной. Для многочлена оказывается неверной. Для многочлена 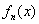 степени степени 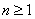 не существует обратного не существует обратного 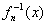 многочлена: многочлена: 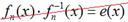 . .
Вроде бы для многочлена 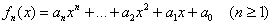 есть «подходящая» дробь есть «подходящая» дробь 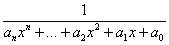 , дающая в произведении единичный элемент, но она
не является многочленом по определению. В то время как элемент , дающая в произведении единичный элемент, но она
не является многочленом по определению. В то время как элемент 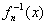 должен обязательно принадлежать множеству должен обязательно принадлежать множеству 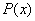 . .
Но это не значит, что многочлены нельзя делить!
 3.3. Деление многочленов 3.3. Деление многочленов
 3.1. Сложение и умножение многочленов 3.1. Сложение и умножение многочленов
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих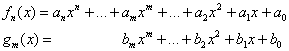
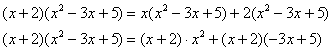
 3.3. Деление многочленов
3.3. Деление многочленов 3.1. Сложение и умножение многочленов
3.1. Сложение и умножение многочленов