1.5.6. Как приводить дроби к общему знаменателю?
Выше я привёл «прямую» формулу приведения: 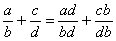 , но она далеко
не всегда рациональна. Так, при сложении , но она далеко
не всегда рациональна. Так, при сложении 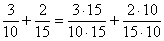 внизу получается 150,
что многовато. Нельзя ли уменьшить это значение? Смотрим на знаменатели дробей: 10, 15 и замечаем, что оба они делятся на
5. Делим на 5 нашего монстра: внизу получается 150,
что многовато. Нельзя ли уменьшить это значение? Смотрим на знаменатели дробей: 10, 15 и замечаем, что оба они делятся на
5. Делим на 5 нашего монстра: 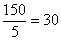 – и полученное число должно
подойти в качестве общего знаменателя. И в самом деле, 30 делится и на 10 и на 15. Делим – и полученное число должно
подойти в качестве общего знаменателя. И в самом деле, 30 делится и на 10 и на 15. Делим 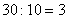 – и домножаем на три числитель и знаменатель первой дроби: – и домножаем на три числитель и знаменатель первой дроби: 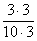 . Теперь делим . Теперь делим 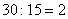 – и
домножаем на два оба этажа второй дроби: – и
домножаем на два оба этажа второй дроби: 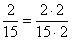 . .
Таким образом: 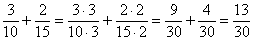
…много я тут наговорил, но на самом деле такой подбор выполнятся устно, и не всё так сложно! Принцип прост: общий
знаменатель должен делиться на знаменатель каждой дроби (само собой) и быть как можно меньше (по возможности).
Запишу общую формулу (не пугаемся):
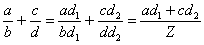 , где , где 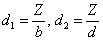 – дополнительные множители; общий знаменатель – дополнительные множители; общий знаменатель 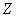 должен делиться на должен делиться на 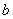 и на и на
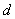 и быть как можно меньше. и быть как можно меньше.
Рассмотрим разность 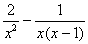 . Здесь можно снова использовать прямую
формулу . Здесь можно снова использовать прямую
формулу 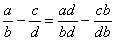 с общим знаменателем с общим знаменателем 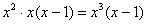 . Но есть более рациональная версия: . Но есть более рациональная версия: 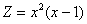 – она делится и на знаменатель первой дроби и на знаменатель второй. Выполняем это
деление – рассчитываем дополнительные множители: – она делится и на знаменатель первой дроби и на знаменатель второй. Выполняем это
деление – рассчитываем дополнительные множители: 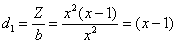 , , 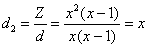 . Таким образом, по формуле: . Таким образом, по формуле:
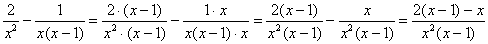 , вверху, как правило, раскрывают скобки и приводят подобные слагаемые: , вверху, как правило, раскрывают скобки и приводят подобные слагаемые: 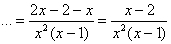
В качестве проверки выполним обратное действие – оно называется почленным делением числителя на знаменатель:
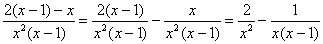 – в результате получена исходная разность, что и
требовалось проверить. – в результате получена исходная разность, что и
требовалось проверить.
Нередко приходится приводить несколько дробей, например: 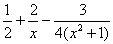 .
Здесь используются аналогичные формулы. Можно задействовать «прямой» вариант: .
Здесь используются аналогичные формулы. Можно задействовать «прямой» вариант: 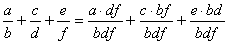 с общим знаменателем с общим знаменателем 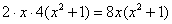 ,
но нельзя ли его уменьшить? В данном случае можно: ,
но нельзя ли его уменьшить? В данном случае можно: 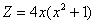 – легко
видеть, что он делится на знаменатель каждой дроби и является минимальным. Вычислим дополнительные
множители – легко
видеть, что он делится на знаменатель каждой дроби и является минимальным. Вычислим дополнительные
множители 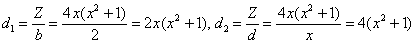 , , 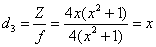 и по формуле и по формуле 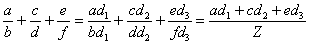 : :
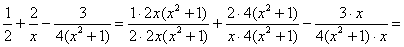
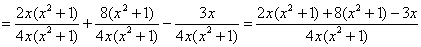 , допилим позже. , допилим позже.
Проверка состоит в почленном делении числителя на знаменатель, многое тут сократится: 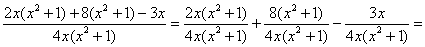 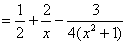 – и в результате мы
получили исходную сумму. – и в результате мы
получили исходную сумму.
Тренируемся самостоятельно:
Задание 2
а) Перевести десятичные дроби в обыкновенные и, если это возможно, сократить их: 0,2; –1,34; 2,625. Выполнить проверку делением
числителя на знаменатель.
Выполнить следующие действия:
б) 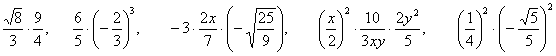
в) разделить минус три на три седьмых, шесть тринадцатых на два, одиннадцать пятых на две трети.
г) 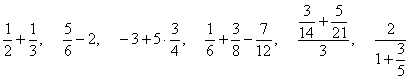
д) Привести к общему знаменателю: 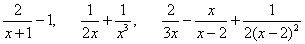 . .
е) Упростить дроби: 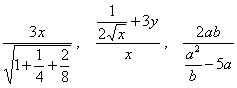 . .
Решения и ответы в конце книги.
 1.6. Одночлены, многочлены и другие члены 1.6. Одночлены, многочлены и другие члены
 1.5.5. Сложение дробей 1.5.5. Сложение дробей
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики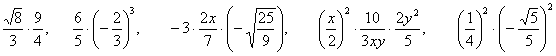
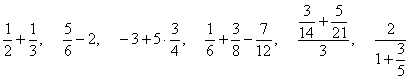
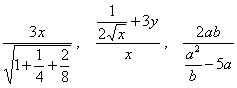 .
. 1.6. Одночлены, многочлены и другие члены
1.6. Одночлены, многочлены и другие члены 1.5.5. Сложение дробей
1.5.5. Сложение дробей