|
Ваш репетитор, справочник и друг!
|
2.8. Понятие системыНе так давно нам встретилась фигурная скобка Система – это множество условий, которые должны выполняться вместе. Решение системы (если оно существует) удовлетворяет ВСЕМ условиям системы. Решим, например, систему уравнений Если у системы нет решений, то её называют несовместной. Так, несовместной является следующая система неравенств: Система может состоять из разнородных условий: Более того в качестве условий могут выступать не только уравнения и неравенства: Ну и, конечно, не забываем о системе физических упражнений, чтобы не «закостенеть» перед монитором :). Тридцать отжиманий, двадцать приседаний и пару километров трусцой. А если что-то не выполните, то, увы, это уже будет не система( Таким образом, с помощью системы можно решить разные задачи! Например, двойное
неравенство Решение первого неравенства изобразим сверху, а второго – снизу: Решением системы является общий промежуток: Сколько может быть условий в системе? Да сколько угодно. Сколько может быть решений у системы? Ни одного, одно, несколько, много или бесконечно много :). И решить систему – это значит найти ВСЕ решения либо доказать, что их нет. Впрочем, иногда нужно найти хоть какое-то решение системы. Возможно, у вас ещё возник вопрос: а где же те ужасные школьные уравнения и неравенства с корнями и всякими синусами? Забудьте! В высшей математике они практически не потребуются. Достаточно повторить лишь самые простые.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Кратчайший курс школьной математики
Кратчайший курс школьной математики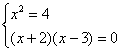 . Это означает, что
нам нужно найти ТАКИЕ значения «икс», которые удовлетворяют каждому уравнению системы. Или доказать, что их не существует.
Очевидно, что
. Это означает, что
нам нужно найти ТАКИЕ значения «икс», которые удовлетворяют каждому уравнению системы. Или доказать, что их не существует.
Очевидно, что 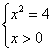 – решением этой
системы является значение
– решением этой
системы является значение  – решением этой системы являются числа
– решением этой системы являются числа 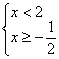

 2.9. Уравнения и неравенства с несколькими переменными
2.9. Уравнения и неравенства с несколькими переменными 2.7. Уравнения и неравенства с модулем
2.7. Уравнения и неравенства с модулем