2.9. Уравнения и неравенства с несколькими переменными
До сих пор мы рассматривали только одну переменную – «икс». Но совершенно понятно, что уравнение или неравенство может содержать и
несколько различных переменных. Например, две. Добавим вторую сакральную букву – «игрек»:
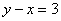
Данное уравнение имеет бесконечно много решений, например: 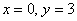 или или 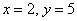 . Каждая пара значений обращает
уравнение в верное числовое равенство, а значит, действительно является решением. Возникает вопрос: как отыскать ВСЕ решения?
Очень просто. Оставим в левой части только игрек, для этого перенесём «икс» направо, сменив у него знак. Да, с уравнением
нескольких переменных можно делать практически всё то же самое: . Каждая пара значений обращает
уравнение в верное числовое равенство, а значит, действительно является решением. Возникает вопрос: как отыскать ВСЕ решения?
Очень просто. Оставим в левой части только игрек, для этого перенесём «икс» направо, сменив у него знак. Да, с уравнением
нескольких переменных можно делать практически всё то же самое:
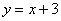
И теперь хорошо видно, что «игрек» на три больше, чем «икс». Таким образом, мы получили закон, по которому каждому
значению 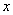 ставится в соответствие строго определённое значение ставится в соответствие строго определённое значение
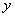 . И, пользуясь этим законом, легко найти любую пару решений. . И, пользуясь этим законом, легко найти любую пару решений.
Как и младший брат, уравнение с двумя переменными может иметь единственное решение, например: 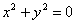 или не иметь действительных решений вовсе: или не иметь действительных решений вовсе: 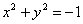
Популярная система, а-ля 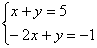 , может иметь единственное решение,
бесконечно много решений или же не иметь их совсем. Давайте вспомним этот школьный метод решения: из 1-го уравнения выразим «игрек» (можно «икс»): , может иметь единственное решение,
бесконечно много решений или же не иметь их совсем. Давайте вспомним этот школьный метод решения: из 1-го уравнения выразим «игрек» (можно «икс»): 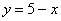 , и подставим во 2-е уравнение: , и подставим во 2-е уравнение: 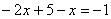 . Приводим подобные слагаемые: . Приводим подобные слагаемые:
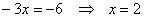 – подставим в 1-е уравнение: – подставим в 1-е уравнение: 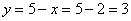 . .
Таким образом, пара 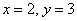 является единственным решением системы.
Мысленно подставьте эти значения в каждое уравнение системы и убедитесь в том, что они «подходят» и там и там. является единственным решением системы.
Мысленно подставьте эти значения в каждое уравнение системы и убедитесь в том, что они «подходят» и там и там.
В курсе высшей математики мы изучим эти системы досконально, а также познакомимся со смыслом и методом решения
соответствующих неравенств: 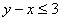 и их систем: и их систем: 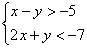 , в которых работают те же
«фишки». Ну а пока есть дела понасущнее – возвращаемся к тому самому закону, который чудесным образом возник в ходе решения уравнения , в которых работают те же
«фишки». Ну а пока есть дела понасущнее – возвращаемся к тому самому закону, который чудесным образом возник в ходе решения уравнения 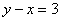 : :
 3.1. Понятие функции 3.1. Понятие функции
 2.8. Понятие системы 2.8. Понятие системы
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики 3.1. Понятие функции
3.1. Понятие функции 2.8. Понятие системы
2.8. Понятие системы