Ваш репетитор, справочник и друг!

Кратчайший курс школьной математики

2.2. Преобразование уравнений

В этом параграфе мы поговорим о том, что можно делать с уравнениями, а чего делать нельзя. И что можно, но осторожно.

Весьма содержательный пример встретился в Задании 5:

В любой части уравнения (и слева, и справа) можно выносить множители за скобки и скобки раскрывать:

В любой части можно приводить подобные слагаемые:

Части уравнения можно менять местами, они абсолютно равноценны:

Любое слагаемое можно перенести в другую часть, сменив у него знак:

Обе части можно умножать / делить на одно и то же число, отличное от нуля:

И обязательно проверка: подставим найденное значение в исходное уравнение :

– в результате получено верное равенство, значит, действительно является корнем данного уравнения. И здесь я хочу сформулировать вторую практическую аксиому:

Если что-то можно проверить, то стараемся это проверить

…прямо таки жизненный и даже философский принцип получился :). В важных задачах лучше проверять даже устные вычисления – например, с помощью калькуляторов, которые приложены к этому курсу. Ибо никто не застрахован от ошибок по «глюку».

Кроме того, есть многочисленные онлайн сервисы для решения различных задач. Но тут я должен предостеречь: 1) они могут работать с ошибками (а кто их вообще создал?), 2) машинное решение некоторых задач выглядит вычурно и неуклюже – так не станет решать ни один вменяемый человек, 3) и поэтому ответы могут быть представлены в другом, «нечеловеческом» виде :)) Однако для проверки такие сервисы (качественные) во многих случаях годятся.
Следующий момент касается уравнений вида (пусть и не равны 0). Для краткости я буду называть это правило правилом пропорции, сформулирую его в вольном стиле: множители, которые находятся вверху, можно «сбрасывать» на нижний этаж противоположной части. И обратно: множители, которые находятся внизу, можно «поднимать» в числитель противоположной части.

Крутим-вертим:
и так далее – смотря что вам нужно выразить в той или иной задаче.

Справка: – значок следствия («из этого следует это»)

На практике чаще выполняют «поднятие» множителей – для того, чтобы избавиться от дробей, при этом особое внимание следует проявить, если «поднимаемый» множитель может обращаться в ноль. Рассмотрим уравнение:

Первое действие очевидно – поднимаем сумму на верх правой части:
, но здесь следует иметь в виду, что значение не может являться корнем уравнения, ибо сумма-то была в знаменателе.

Берём это на заметку и продолжаем. Раскрываем скобки в правой части:
,

после чего собираем все «иксы» в левой части, а константы – в правой, не забывая при переносе слагаемых сменить у них знаки:
,

приводим подобные слагаемые:

и умножаем обе части на -1:

Проверка: подставим найденное значение в исходное уравнение:

– в результате получено верное равенство, значит, действительно является корнем уравнения .
Теперь о том, чего делать нельзя: нельзя сокращать на множитель, который содержит переменную. Это ведёт к потере корней. Запишите, запомните, зазубрите! Так, если мы сократим уравнение на «икс», то потеряем корень (который обращает уравнение в верное равенство ).
И даже здесь: – сокращать на НЕ НАДО – поскольку уравнение имеет два комплексных корня, которые мы потеряем. Хоть это и не принципиально для решения школьных задач, но все равно является дурным тоном.

Итак, множители с переменными не сокращаем!

Обе части уравнения можно возвести в степень, но при этом могут появиться посторонние корни. Так, чтобы решить уравнение нужно возвести обе его части в квадрат: , и полученное уравнение будет иметь два корня: . Однако исходному уравнению удовлетворяет лишь значение , что выясняется прямой подстановкой. Корень же является посторонним, ибо:

– неверное равенство. Этот корень также можно отфильтровать из тех соображений, что арифметический квадратный корень неотрицателен: .
Следует отметить, что посторонних корней может и не оказаться, всё зависит от того или иного примера. Но заморачивать тут не нужно – проверяем и выясняем!

Кстати, что это за уравнение и как отыскать его корни? …Многие вспомнили, что это мегапопулярное:

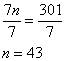
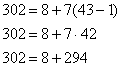
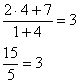
2.3. Квадратное уравнение

2.1. Понятие уравнения. Простейшие примеры

| Оглавление |