2.3. Квадратное уравнение
Данное уравнение имеет вид 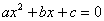 , где , где 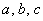 – числа, при этом – числа, при этом 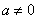 . .
Начнём с частных случаев. Если коэффициенты «бэ» и «цэ» равны нулю, то уравнение 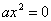 можно сократить на «а» и записать его виде можно сократить на «а» и записать его виде 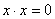 . Это уравнение имеет два совпавших или, как говорят математики, кратных корня: . Это уравнение имеет два совпавших или, как говорят математики, кратных корня: 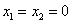 . .
Если нулю равен коэффициент «бэ», то квадратное уравнение принимает вид 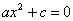 и тут две ветки. Если оба коэффициента положительны или оба отрицательны, то уравнение
имеет два комплексных корня, типичный пример уже был выше: и тут две ветки. Если оба коэффициента положительны или оба отрицательны, то уравнение
имеет два комплексных корня, типичный пример уже был выше: 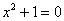 .
Если же коэффициенты разных знаков, то дело сводится к уравнению .
Если же коэффициенты разных знаков, то дело сводится к уравнению 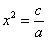 , которое имеет два корня: , которое имеет два корня: 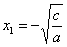 и и 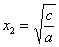 . Так, уравнение . Так, уравнение 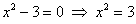 имеет корни имеет корни 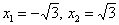 , в чём легко
убедиться прямой подстановкой. , в чём легко
убедиться прямой подстановкой.
И, наконец, сладкий случай, когда 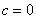 : : 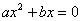 – выносим «икс» за скобки: – выносим «икс» за скобки: 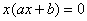 и корни выкатываются на блюдечко с голубой каёмочкой: и корни выкатываются на блюдечко с голубой каёмочкой: 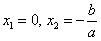 , даже пример приводить неловко :) , даже пример приводить неловко :)
Теперь общий случай 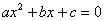 , где все коэффициенты
отличны от нуля. , где все коэффициенты
отличны от нуля.
И сразу то самое уравнение: 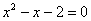 . .
Чтобы решить такое уравнение, нужно вычислить дискриминант – по формуле:
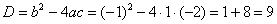
На втором шаге извлекаем квадратный корень из дискриминанта:
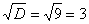
Если корень получился «плохим», например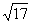 , то без паники.
Перепроверьте дискриминант. Если квадратное уравнение появилось в ходе решения задачи, то, возможно, вы допустили ошибку где-то ранее. Но
бывает и так, что в условии опечатка либо… так и было задумано! Потому что в любом случае квадратное уравнение разрешимо и имеет
ровно два корня: , то без паники.
Перепроверьте дискриминант. Если квадратное уравнение появилось в ходе решения задачи, то, возможно, вы допустили ошибку где-то ранее. Но
бывает и так, что в условии опечатка либо… так и было задумано! Потому что в любом случае квадратное уравнение разрешимо и имеет
ровно два корня:
1) Если 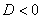 , то уравнение имеет два сопряжённых комплексных корня. Это выходит за рамки школьной программы,
но для страждущих я ещё раз поставил ссылку :) , то уравнение имеет два сопряжённых комплексных корня. Это выходит за рамки школьной программы,
но для страждущих я ещё раз поставил ссылку :)
2) Если 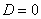 , то уравнение имеет два совпавших (кратных)
действительных корня, которые определяются по формуле , то уравнение имеет два совпавших (кратных)
действительных корня, которые определяются по формуле 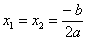 . .
3) И, наконец, 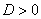 . Здесь уравнение имеет два действительных
корня: . Здесь уравнение имеет два действительных
корня:
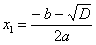 , , 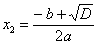 – обычно их располагают в порядке возрастания. – обычно их располагают в порядке возрастания.
В нашем примере:
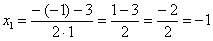 и и 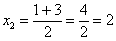
Не забываем о проверке! Самостоятельно подставьте найденные значения в уравнение 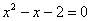 и убедитесь, что получаются верные равенства. и убедитесь, что получаются верные равенства.
Следует отметить, что рассмотренный алгоритм формально применИм и для любого частного случая, которые мы разобрали в начале параграфа.
А в его заключение – ОЧЕНЬ важная и обещанная вещь:
В практических задачах часто требуется разложить квадратный трёхчлен 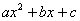 на множители. Для этого нужно решить уравнение на множители. Для этого нужно решить уравнение 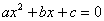 и воспользоваться формулой: и воспользоваться формулой:
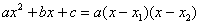 , где , где 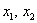 – корни данного уравнения. – корни данного уравнения.
Так, уравнение 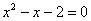 имеет корни имеет корни 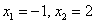 , и по формуле: , и по формуле:
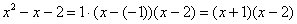 – самостоятельно перемножьте
суммы и убедитесь, что получается исходный трёхчлен. Это, кстати, легко сделать устно. – самостоятельно перемножьте
суммы и убедитесь, что получается исходный трёхчлен. Это, кстати, легко сделать устно.
 2.4. Неравенства 2.4. Неравенства
 2.2. Преобразование уравнений 2.2. Преобразование уравнений
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики 2.4. Неравенства
2.4. Неравенства 2.2. Преобразование уравнений
2.2. Преобразование уравнений