|
Ваш репетитор, справочник и друг!
|
1.8.2. Геометрическая прогрессияНаверняка вы слышали выражение, что что-то растёт в геометрической прогрессии. Это означает очень быстрый рост – рост в разЫ. А если это что-что в геометрической прогрессии убывает, значит, оно с кратным ускорением стремится к нулю. Геометрическая прогрессия – это числовая последовательность, первый член которой Если Любой член геометрической прогрессии легко определить по формуле Сумма первых В качестве примера вычислим сумму Однако особый интерес представляет бесконечно убывающая геометрическая прогрессия. Это прогрессия с бесконечным количеством
членов и основанием Но главная «фишка» состоит в том, что сумма бесконечного количества членов… равна конечному числу! И особо приятно, что для
расчёта этой суммы существует очень простая формула: Символические задачки для самостоятельного решения: Задание 5 а) Вычислить сумму арифметической прогрессии (2 штуки):
б) Вычислить сумму геометрической прогрессии (3 штуки):
Решения с комментариями в конце книги
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Кратчайший курс школьной математики
Кратчайший курс школьной математики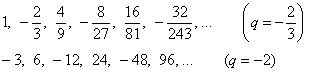
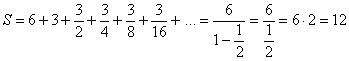 – главное, правильно упростить
– главное, правильно упростить  2.1. Понятие уравнения. Простейшие примеры
2.1. Понятие уравнения. Простейшие примеры 1.8.1. Арифметическая прогрессия
1.8.1. Арифметическая прогрессия