3.1. Понятие функции
Функция одной (независимой) переменной – это правило 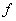 (зависимость, закон) по которому каждому допустимому значению (зависимость, закон) по которому каждому допустимому значению 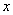 ставится в соответствие одно и только одно значение ставится в соответствие одно и только одно значение 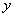 . Стандартная запись: . Стандартная запись: 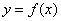
Переменная 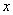 называется независимой переменной или аргументом. называется независимой переменной или аргументом.
Переменная 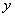 называется зависимой переменной и, кроме того, под «игреком» также подразумевают функцию. называется зависимой переменной и, кроме того, под «игреком» также подразумевают функцию.
Таким образом, функцию можно записать так: 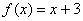 , либо так: , либо так: 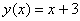 , либо так: , либо так: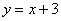 , для краткости чаще будем использовать последний вариант. Данное правило увеличивает каждое значение «икс» на три. Например: , для краткости чаще будем использовать последний вариант. Данное правило увеличивает каждое значение «икс» на три. Например: 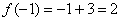 . .
Следующий закон удваивает каждое значение «икс»: 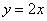 . А вот эта функция возводит «иксы» в квадрат: . А вот эта функция возводит «иксы» в квадрат: 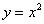 . И так далее, различных функций – просто тьма. . И так далее, различных функций – просто тьма.
Функцию также записывают в виде уравнения 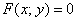 (стандартный вид). Возьмём ту же функцию (стандартный вид). Возьмём ту же функцию 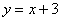 и перебросим все члены налево: и перебросим все члены налево: 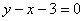 . В таких случаях говорят, что функция задана неявно или в неявном виде. Потому что сразу не понятно, что делает эта функция :) . В таких случаях говорят, что функция задана неявно или в неявном виде. Потому что сразу не понятно, что делает эта функция :)
Множество допустимых значений «икс» называют областью определения функции – это те значения, для которых определены «игреки». Область определения обозначают следующим образом: 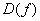 или или 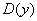 . .
Областью определения всех перечисленных выше функций является любое «икс», т.е. все действительные значения: 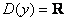 . Но этим может похвастаться далеко не каждая функция. . Но этим может похвастаться далеко не каждая функция.
Так, функция 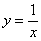 определена для всех «икс» кроме нуля: определена для всех «икс» кроме нуля:
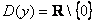 , вместо значка исключения ( , вместо значка исключения (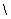 ) здесь также можно использовать объединение двух интервалов: ) здесь также можно использовать объединение двух интервалов: 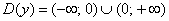
Функция 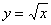 определена лишь для неотрицательных значений «икс»: определена лишь для неотрицательных значений «икс»:
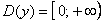
И в заключение параграфа кратко об обратной функции 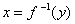 – эта функция «возвращает» исходное значение «икс». Например, для – эта функция «возвращает» исходное значение «икс». Например, для 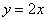 обратной является: обратной является: 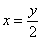 . Следует отметить, что далеко не каждая функция обратима, так, для функции . Следует отметить, что далеко не каждая функция обратима, так, для функции 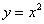 обратная функция не определена, ибо если известно, что обратная функция не определена, ибо если известно, что 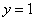 , то не понятно, как это значение получилось: то ли при возведении , то не понятно, как это значение получилось: то ли при возведении 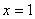 в квадрат, то ли при возведении в квадрат, то ли при возведении 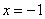 . .
 3.2. График функции в декартовой системе координат 3.2. График функции в декартовой системе координат
 2.9. Уравнения и неравенства с несколькими переменными 2.9. Уравнения и неравенства с несколькими переменными
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики 3.2. График функции в декартовой системе координат
3.2. График функции в декартовой системе координат 2.9. Уравнения и неравенства с несколькими переменными
2.9. Уравнения и неравенства с несколькими переменными