3.2. График функции в декартовой системе координат
Это графическое изображение функциональной зависимости. График функции 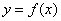 обычно
строят в прямоугольной (декартовой) системе координат. И посему сначала нужно построить саму систему. Для этого выбираем начало координат обычно
строят в прямоугольной (декартовой) системе координат. И посему сначала нужно построить саму систему. Для этого выбираем начало координат 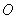 и чертим координатные оси. Ось и чертим координатные оси. Ось 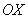 называется осью абсцисс, а ось называется осью абсцисс, а ось 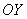 – осью ординат.
Угол между осями равен – осью ординат.
Угол между осями равен 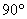 (прямой угол), отсюда и название – прямоугольная
система. (прямой угол), отсюда и название – прямоугольная
система.
Итак, подписываем оси и задаём размерность по ним. При оформлении чертежа в тетради наиболее популярны следующие масштабы:

Для того чтобы задать масштаб, достаточно нарисовать ноль и две единицы.
НЕ НУЖНО «строчить из пулемёта»:  . Ибо координатная плоскость – не
памятник Декарту, а студент – не голубь J . Ибо координатная плоскость – не
памятник Декарту, а студент – не голубь J
По возможности старайтесь использовать масштаб: 1 единица = 2 клетки (чертеж слева) Однако время от времени случается так, что чертеж
не вмещается на тетрадный лист – и тогда масштаб уменьшаем: 1 единица = 1 клетка (чертеж справа). Редко, но бывает, что масштаб чертежа
приходится уменьшать (или увеличивать) ещё больше.
И на всякий пожарный повторим, как отмечать точки. Любая точка плоскости однозначно определяется двумя координатами, при этом
1-я координата – это строго «иксовая» координата (по оси 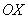 ), а 2-я координата – это строго «игрековая» координата (по оси ), а 2-я координата – это строго «игрековая» координата (по оси 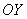 ) В качестве примере отмечу точки ) В качестве примере отмечу точки 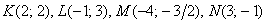 : :

И да, координатные оси делят координатную плоскость на четыре координатных четверти, их я занумеровал римскими числами (общепринятый порядок номеров).
На координатной плоскости можно построить много чего интересного, но сейчас нас интересуют графики функций. Чтобы построить график 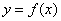 обычно требуется найти несколько (или чуть больше) точек,
координаты которых удовлетворяют данному закону, отметить эти точки на чертеже и аккуратно соединить линией. При этом важно знать
принципиальный вид графика той или иной функции. Все функции можно разделить на несколько больших групп, и сейчас мы вспомним основные
семейства: обычно требуется найти несколько (или чуть больше) точек,
координаты которых удовлетворяют данному закону, отметить эти точки на чертеже и аккуратно соединить линией. При этом важно знать
принципиальный вид графика той или иной функции. Все функции можно разделить на несколько больших групп, и сейчас мы вспомним основные
семейства:
 3.3. Линейная функция 3.3. Линейная функция
 3.1. Понятие функции 3.1. Понятие функции
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики

 3.3. Линейная функция
3.3. Линейная функция 3.1. Понятие функции
3.1. Понятие функции