3.3. Линейная функция
Имеет вид 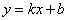 , где , где 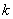 и и 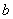 – константы (числа). Графиком линейной
функции является прямая. Для её построения достаточно знать две точки. Так, для функции – константы (числа). Графиком линейной
функции является прямая. Для её построения достаточно знать две точки. Так, для функции 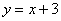 удобно выбрать значение удобно выбрать значение 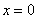 и найти и найти 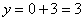 , и, например, для , и, например, для 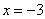 вычислить вычислить 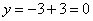 . Отмечаем найденные точки . Отмечаем найденные точки 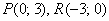 на чертеже и аккуратно, по линейке проводим прямую: на чертеже и аккуратно, по линейке проводим прямую:
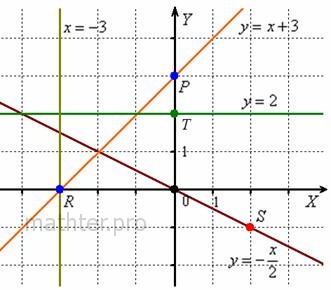 Прямая вида Прямая вида 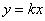 проходит через начало координат и называется прямой пропорциональностью. Для её построения нужно
найти одну точку. Так, для прямой проходит через начало координат и называется прямой пропорциональностью. Для её построения нужно
найти одну точку. Так, для прямой 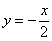 удобно выбрать удобно выбрать 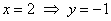 . Отмечаем на чертеже точку . Отмечаем на чертеже точку 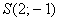 и порядок! и порядок!
Коэффициент 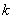 называется угловым коэффициентом
прямой. Если называется угловым коэффициентом
прямой. Если 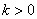 , то график идёт «снизу вверх», например, график , то график идёт «снизу вверх», например, график 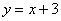 . Если . Если 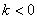 , то график идёт «сверху вниз», например, , то график идёт «сверху вниз», например, 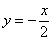 . .
Чем больше 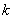 по
модулю, тем круче идёт график, и наоборот, чем по
модулю, тем круче идёт график, и наоборот, чем 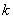 по
модулю меньше – тем график более пологий. Так, график по
модулю меньше – тем график более пологий. Так, график 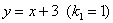 имеет более
крутой наклон, нежели график имеет более
крутой наклон, нежели график 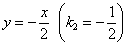 , ибо , ибо 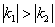 . .
Если 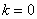 , то получаем функцию-константу: , то получаем функцию-константу: 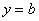 . Как её понять неформально? «Игрек» ВСЕГДА (при любом «икс») равен одному и тому же числу.
Данная прямая параллельна оси . Как её понять неформально? «Игрек» ВСЕГДА (при любом «икс») равен одному и тому же числу.
Данная прямая параллельна оси 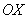 и проходит через точку и проходит через точку 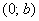 , так, прямая , так, прямая 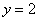 проходит через точку проходит через точку 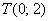 . Функция . Функция 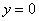 задаёт ось задаёт ось 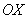 – запомните этот важный факт! – запомните этот важный факт!
И остались у нас прямые, параллельные оси 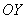 . Увы, их нельзя задать с
помощью функции . Увы, их нельзя задать с
помощью функции 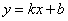 , но зато можно с помощью общего уравнения прямой: , но зато можно с помощью общего уравнения прямой: 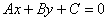
Если 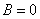 , то получается уравнение вида , то получается уравнение вида 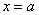 . Оно задаёт прямую, которая параллельна оси . Оно задаёт прямую, которая параллельна оси 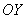 и проходит через точку и проходит через точку 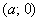 . Так, прямая . Так, прямая 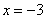 проходит через точку проходит через точку 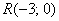 . И, в частности, уравнение . И, в частности, уравнение 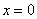 задаёт саму ось задаёт саму ось 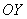 . .
Если же 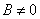 , то из общего уравнения , то из общего уравнения 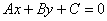 легко выразить функцию: легко выразить функцию:
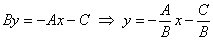 , которая описывает все остальные случаи. , которая описывает все остальные случаи.
 3.4. СтепеннАя функция 3.4. СтепеннАя функция
 3.2. График функции в декартовой системе координат 3.2. График функции в декартовой системе координат
| Оглавление |
|