3.4. СтепеннАя функция
На самом деле эту функцию мы начали разбирать в предыдущем параграфе, где «икс» находился в первой степени. Но степень может быть и больше, и
меньше или вообще быть дробной. Рассмотрим наиболее распространенные случаи:
Функция вида 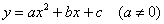 называется квадратичной функцией, а её
график – параболой. Если называется квадратичной функцией, а её
график – параболой. Если 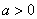 , то ветви параболы «смотрят» вверх, если , то ветви параболы «смотрят» вверх, если 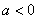 , то вниз. , то вниз.
Простейшая парабола вам хорошо известна: 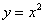 (см. ниже).
Обратите внимание, что график этой функции симметричен относительно оси (см. ниже).
Обратите внимание, что график этой функции симметричен относительно оси 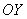 . Такие функции называют чётными. Аналитически чётность выражается условием . Такие функции называют чётными. Аналитически чётность выражается условием 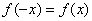 . Проверим на чётность нашу функцию, для этого ВМЕСТО . Проверим на чётность нашу функцию, для этого ВМЕСТО 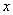 подставим подставим 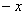 : :
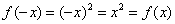 , значит, функция , значит, функция 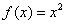 – чётная. – чётная.
В общем случае квадратичная функция чётной не является, но симметрию самой параболы никто не отменял и этим удобно пользоваться на
практике.
Как быстро построить любую параболу? Очевидно, сначала выгодно найти её вершину, а затем – несколько пар симметричных точек.
Посмотрим, как это происходит на примере функции 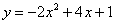 : :
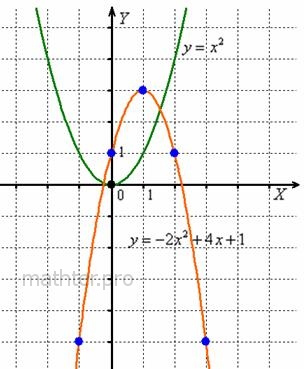 Сначала находим вершину, для этого берём производную и приравниваем её к нулю: Сначала находим вершину, для этого берём производную и приравниваем её к нулю: 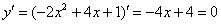
Найдём корень уравнения: 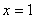 – тут и находится вершина, её «игрек»: – тут и находится вершина, её «игрек»:
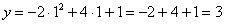
Теперь найдём опорные точки (обычно хватает четырёх), при этом используем симметрию параболы и принцип «влево-вправо»:
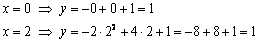
Внимание! Для проверки рассчитываем и то, и то значение, они должны совпасть!
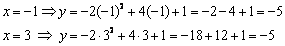
Перечисленные действия обычно выполняются устно или на черновике, а результаты заносятся в табличку:

Осталось отметить найденные точки на чертеже и АККУРАТНО соединить их линией. Рассмотренный алгоритм не является обязательным и в простых
случаях вершину параболы можно обнаружить методом «практического тыка», просто перебирая точки. Особенно, если у вас нелады с производными (их
рассмотрим в курсе вышмата).
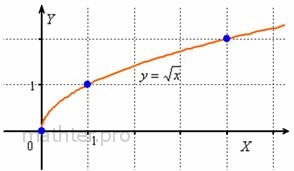 График функции График функции 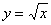 представляет собой ветвь параболы, которая «лежит на боку»: представляет собой ветвь параболы, которая «лежит на боку»:
Как уже отмечалось, эта функция определена лишь для неотрицательных «икс»: 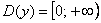 , ,
и для построения графика удобно использовать следующие опорные точки:
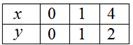
График функции 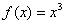 называется
кубической параболой. Данная функция симметрична относительно начала координат, и такие функции называют
нечётными. Аналитически нечётность выражается условием называется
кубической параболой. Данная функция симметрична относительно начала координат, и такие функции называют
нечётными. Аналитически нечётность выражается условием 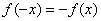 . Проверим нашу
функцию на нечётность, для этого ВМЕСТО . Проверим нашу
функцию на нечётность, для этого ВМЕСТО 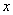 подставим подставим 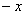 : : 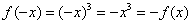 , ч.т.п. , ч.т.п.
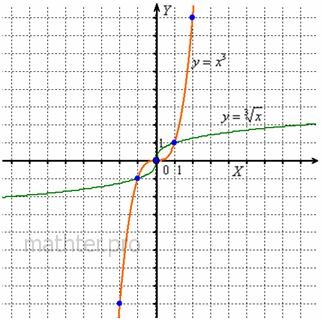
Для построения кубической параболы достаточно отметить точки:
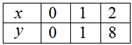
после чего воспользоваться симметрией или как раз нечётностью функции:
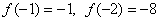 . .
График функции 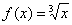 представляет собой кубическую параболу, «лежащую на
боку». В отличие от представляет собой кубическую параболу, «лежащую на
боку». В отличие от 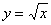 , эта функция определена для всех «икс»: , эта функция определена для всех «икс»: 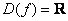 и тоже является нечётной, ибо «минус» преспокойно выносится вперёд: и тоже является нечётной, ибо «минус» преспокойно выносится вперёд:
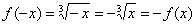
График произвольного корня 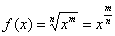 с дробным показателем следует
строить, имея в виду область определения того или иного корня. Так, функция с дробным показателем следует
строить, имея в виду область определения того или иного корня. Так, функция 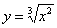 , как и , как и 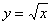 , определена только для
неотрицательных «икс»: , определена только для
неотрицательных «икс»: 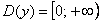 и для построения её графика
придётся найти несколько значений приближенно: и для построения её графика
придётся найти несколько значений приближенно:
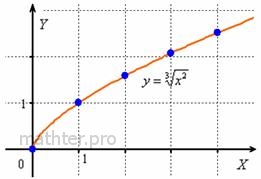 
Такие значения на математическом жаргоне называют «плохими», но что поделать….
Данная функция не является чётной или нечётной, поскольку она не определена для отрицательных «икс», а значит, условие 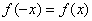 либо либо 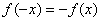 просто не может выполняться. просто не может выполняться.
График функции 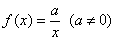 представляет собой
гиперболу. Да, это тоже степенная функция! Ибо представляет собой
гиперболу. Да, это тоже степенная функция! Ибо 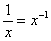 .
Если .
Если 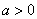 , то ветви гиперболы лежат в 1-й и 3-й координатных четвертях, если , то ветви гиперболы лежат в 1-й и 3-й координатных четвертях, если 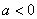 , то во 2-й и 4-й (см. примеры на чертеже ниже). Очевидно, что перед нами нечётная функция,
поскольку: , то во 2-й и 4-й (см. примеры на чертеже ниже). Очевидно, что перед нами нечётная функция,
поскольку: 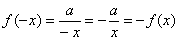 . .
Данная функция не определена в точке 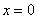 , а
координатные оси являются асимптотами графика – «залезать на них» нельзя! Асимптота, если «на пальцах» – это прямая, к
которой график приближается бесконечно близко, но не пересекает её. , а
координатные оси являются асимптотами графика – «залезать на них» нельзя! Асимптота, если «на пальцах» – это прямая, к
которой график приближается бесконечно близко, но не пересекает её.
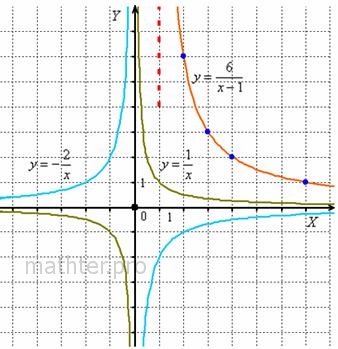
Как быстро построить график гиперболы? (да и не только её)
Во многих случаях удобно поточечное построение, построим, например, правую ветвь 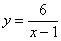 . .
Эта функция не определена в точке 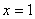 , и
поэтому вертикальная асимптота будет именно здесь. , и
поэтому вертикальная асимптота будет именно здесь.
Найдём несколько опорных точек (подбирая удобные значения «икс»):
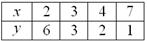
Отмечаем эти точки на чертеже и аккуратно соединяем их линией
Принципиально такую же форму имеют графики 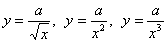 –
только в первом случае гипербола будет иметь одну ветвь, во втором – две ветви, расположенные в 1-й и 2-й координатных четвертях, и третья
гипербола будет похожа на –
только в первом случае гипербола будет иметь одну ветвь, во втором – две ветви, расположенные в 1-й и 2-й координатных четвертях, и третья
гипербола будет похожа на 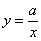 . .
Ну и, конечно, творческие задания, которые нас заждались!
Задание 7
а) Решить графически систему уравнений 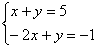 . Догадайтесь сами ;) . Догадайтесь сами ;)
б) Построить график 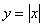 . Вспоминаем, как
раскрывать модуль. . Вспоминаем, как
раскрывать модуль.
в) Проверить функции на чётность / нечётность и построить их графики:
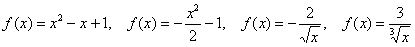 , пожалуй, достаточно. , пожалуй, достаточно.
г) Дано 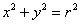 – уравнение окружности с центром в начале координат – уравнение окружности с центром в начале координат
радиуса 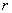 . Выразить функции, определяющие верхнюю и нижнюю полуокружность,
указать их области определения. . Выразить функции, определяющие верхнюю и нижнюю полуокружность,
указать их области определения.
Решения и ответы в конце книги.
 3.5. Графическое решение уравнений и неравенств 3.5. Графическое решение уравнений и неравенств
 3.3. Линейная функция 3.3. Линейная функция
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики Сначала находим вершину, для этого
Сначала находим вершину, для этого  График функции
График функции 



 3.5. Графическое решение уравнений и неравенств
3.5. Графическое решение уравнений и неравенств 3.3. Линейная функция
3.3. Линейная функция