|
Ваш репетитор, справочник и друг!
|
1.7. Свойства степеней и корнейБыстренько вспоминаем, что такое степень – это свёрнутая запись произведения: Повторим важные свойства степеней. Некоторыми из них мы уже вовсю пользовались, в частности: Для того чтобы возвести в степень произведение, нужно возвести в эту степень каждый множитель: Например: Чтобы умножить степени с одинаковыми основаниями, нужно основание оставить таким же, а показатели
сложить: ! Не путать с «похожими» действиями! Для разных оснований Например: Чтобы возвести степень в степень нужно перемножить показатели: Примеры: При переносе степени из знаменателя в числитель (или наоборот) у показателя следует сменить
знак: Да, показатель степени может быть и отрицательным! Например: Деление степеней с одинаковыми основаниями: Например: Разумеется, все правила работают и в обратном направлении, только что вот я «расщепил» степень на множители: Но и это ещё не все секреты! На самом деле корень – это тоже степень: Радикал (корень) можно записать в виде Обращаю ваше внимание, что здесь не проводится никаких алгебраических действий: Например: Корень Главное, уметь приводить дроби к общему знаменателю: Теперь повторим факты, которые касаются именно корней:
Если Корни вида Например: Вы спрОсите, а что не так с корнем
Если Самый популярный случай: Среди «вычислительных» свойств наиболее важнЫ следующие, и ими мы тоже пользовались: Если Если множители отрицательны, то возможны варианты. Так, корень Другие практически значимые свойства: Для натуральных Например: Кроме того, есть и другие свойства, но они тоже не особо актуальны, порешаем лучше примеры: Задание 4 а) Упростить: б) Выполнить действия и записать результат в виде корня: в) Разделить почленно: г) Привести к общему знаменателю: д) Преобразовать: Решения и ответы в конце книги. И местечко тут даже на странице ещё осталось, наверное, какого-то свойства не хватает… или просто умной мысли – подумаю и обязательно добавлю, если надумаю – в следующем переиздании книги :)
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Кратчайший курс школьной математики
Кратчайший курс школьной математики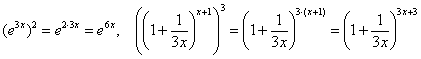 .
.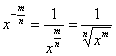 , таким образом:
, таким образом: 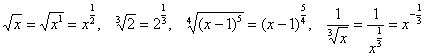
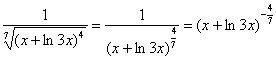 .
.
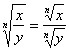
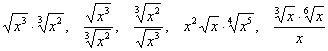 .
.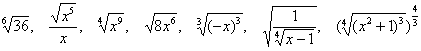
 1.8.1. Арифметическая прогрессия
1.8.1. Арифметическая прогрессия 1.6.4. Как представить сумму в виде произведения?
1.6.4. Как представить сумму в виде произведения?