2.7. Уравнения и неравенства с модулем
Напоминаю, что модуль или абсолютное значение числа – это его расстояние от начала координат, и технически
всё выглядит так, что модуль «уничтожает» возможный знак «минус»: 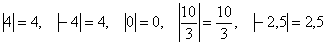 .
Из этого следует, что уравнение .
Из этого следует, что уравнение 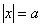 имеет два
корня: имеет два
корня: 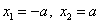 . Если . Если 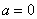 , то корень один. , то корень один.
Зачем нужен модуль? Он используется в умных фразах :). Например: абсолютное значение критической температуры составляет 50 градусов по
Цельсию. По сути, это высказывание представляет собой уравнение 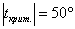 с решениями с решениями 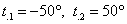 . .
И если эти значения будут превышены по модулю, то, видимо, настанет кирдык.
Если «начинка» модуля более сложная, например, 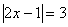 , то
уравнение разруливается по той же схеме, а именно, нужно решить два уравнения: , то
уравнение разруливается по той же схеме, а именно, нужно решить два уравнения:
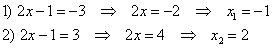
Мысленно подставьте 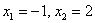 в модуль и убедитесь в том, что это
корни. в модуль и убедитесь в том, что это
корни.
Если «начинка» модуля неотрицательна, то модуль становится ненужным и его можно убрать: 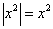 . Также модуль исчезает при возведении его в квадрат: . Также модуль исчезает при возведении его в квадрат: 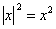 . Разумеется, ВМЕСТО «икс» здесь тоже может быть сложное выражение. . Разумеется, ВМЕСТО «икс» здесь тоже может быть сложное выражение.
Кроме того, уравнение может оказаться ещё более сложным и тогда от модуля избавляются прямо по ходу
решения. В этом случае оно распадается опять же на две ветки по формуле:  . .
ВМЕСТО «икс» может быть сложное выражение, так уравнение 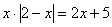 раскладываем на следующие части: раскладываем на следующие части:
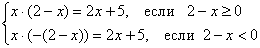
1) Решим первое уравнение, при этом нас устроят только те корни (если они вообще есть), которые удовлетворяют
условию 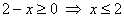 (все поняли переход?): (все поняли переход?):
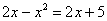
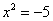 – полученное уравнение не имеет действительных корней. – полученное уравнение не имеет действительных корней.
2) Решим второе уравнение: 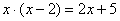 , возможные корни которого должны
соответствовать условию , возможные корни которого должны
соответствовать условию 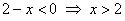 : :
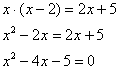
Вычислим дискриминант:
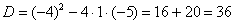 , корень из него , корень из него 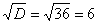 и найдём корни: и найдём корни:
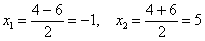
Условию 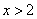 удовлетворяет только второй корень – самостоятельно
подставьте оба значения в исходное уравнение и убедитесь в том, что это действительно так. удовлетворяет только второй корень – самостоятельно
подставьте оба значения в исходное уравнение и убедитесь в том, что это действительно так.
Таким образом, уравнение 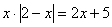 полностью решено, и имеет оно
единственный корень полностью решено, и имеет оно
единственный корень 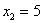 . .
Бывает, модуль возникает в ходе решения других уравнений. Типичный пример:
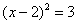
Да, здесь можно возвести в квадрат, привести подобные слагаемые и решить квадратное уравнение. Но зачем? Есть путь короче! Извлекаем
квадратный корень из обеих частей (ещё одно, кстати, действие с уравнениями):
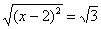 и вспоминаем, что в этом
случае необходимо поставить модуль: и вспоминаем, что в этом
случае необходимо поставить модуль:
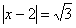
после чего решение входит в знакомую колею:
1) 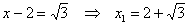 , ,
2) 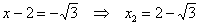 . .
Мысленно подставьте полученные значения в исходное уравнение и убедитесь в том, что они действительно являются корнями.
На очереди неравенства. Давайте прочитаем вслух и вдумаемся в смысл неравенства 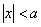 – «икс» по модулю меньше, чем – «икс» по модулю меньше, чем 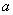 . Это означает, что «икс» принимает значения из интервала . Это означает, что «икс» принимает значения из интервала 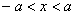 : :

Так, высказыванию нормальная температура по модулю меньше пятидесяти: 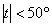 , очевидно, соответствует температурный диапазон , очевидно, соответствует температурный диапазон 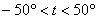 . .
Теперь вдумываемся в неравенство 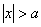 : «икс» по модулю больше,
чем : «икс» по модулю больше,
чем 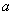 . Это означает, что или . Это означает, что или 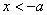 , или , или 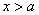 : :
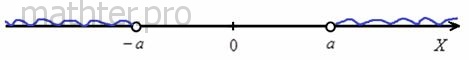
И высказывание температура по модулю больше пятидесяти: 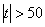 – это и
есть тот самый «кирдык», когда она либо – это и
есть тот самый «кирдык», когда она либо 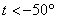 , либо , либо 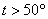 . .
Аналогичные выкладки справедливы для нестрогих неравенств: неравенство 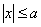 раскрывается через двойное неравенство раскрывается через двойное неравенство 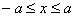 , а неравенство , а неравенство 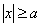 раскрывается через
совокупность неравенств раскрывается через
совокупность неравенств 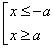 , то есть «икс» или
меньше либо равен , то есть «икс» или
меньше либо равен 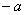 , или больше либо
равен , или больше либо
равен 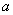 . ВМЕСТО «икс» может быть сложное выражение. . ВМЕСТО «икс» может быть сложное выражение.
Типовой пример встречается при измерении физических величин. Представьте, что вы измеряете линейкой некий объект. Очевидно, что при
выполнении этого физического опыта будет допущена абсолютная погрешность 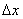 («дельта икс»), но тут есть варианты: вы либо чуть-чуть недомеряете, либо допустите
небольшой перебор. Таким образом, погрешность может оказаться как положительной, так и отрицательной. И здесь будет разумным выдвинуть
следующее требование: абсолютная погрешность измерений («дельта икс»), но тут есть варианты: вы либо чуть-чуть недомеряете, либо допустите
небольшой перебор. Таким образом, погрешность может оказаться как положительной, так и отрицательной. И здесь будет разумным выдвинуть
следующее требование: абсолютная погрешность измерений 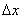 не
должна превышать по модулю одного миллиметра. Эта фраза означает, что не
должна превышать по модулю одного миллиметра. Эта фраза означает, что 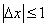 или, что то же самое, погрешность должна находиться в пределах или, что то же самое, погрешность должна находиться в пределах 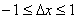 . .
Справка: абсолютная погрешность - это разность между опытным (измеренным) и истинным значением величины: 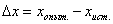 . .
Другая распространённая задача: нормативная масса пачки чая составляет 300 гр. Упаковка проходит контроль, если масса отличается от
норматива на более чем на 2 гр.
Подобную формулировку часто записывают с помощью модуля. Обозначим через 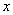 массу произвольной пачки чая. Очевидно, что разность массу произвольной пачки чая. Очевидно, что разность 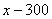 может оказаться как положительной, так и отрицательной, и по модулю это отклонение
не должно превышать двух грамм: может оказаться как положительной, так и отрицательной, и по модулю это отклонение
не должно превышать двух грамм: 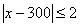 . Или: . Или:
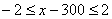 , и теперь нам нужно разрешить это неравенство относительно , и теперь нам нужно разрешить это неравенство относительно 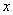 . .
К каждой части двойного неравенства можно прибавить одно и то же число:
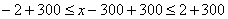
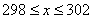 – допустимые границы массы пачки чая. – допустимые границы массы пачки чая.
Пользуюсь случаем, сформулирую ещё одно правило: все три части двойного неравенства можно умножить на одно и то же число, и если
это число отрицательно, то «значки» неравенств следует «развернуть» в противоположную сторону.
Так, для того чтобы решить неравенство 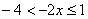 , нужно все его части
умножить на , нужно все его части
умножить на 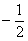 , и поскольку это число отрицательное, то «значки»
неравенств следует «развернуть» в противоположном направлении: , и поскольку это число отрицательное, то «значки»
неравенств следует «развернуть» в противоположном направлении:
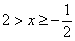 , после чего переписать результат «справа налево»: , после чего переписать результат «справа налево»:
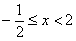 – в привычном порядке, или ещё можно записать: – в привычном порядке, или ещё можно записать: 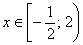 . .
Следует отметить, что правила преобразования двойных неравенств не являются какими-то самостоятельными правилами, они следует из действий с «обычным» неравенством. Но об этом позже.
А сейчас долгожданные задания для самостоятельного решения:
Задание 6
а) Решить уравнения (9 штук):
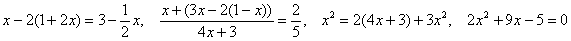 , ,
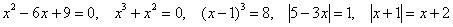
б) Решить неравенства (7 штук):
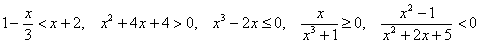 , ,
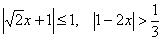 , ответы записать с помощью промежутков , ответы записать с помощью промежутков 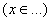 . .
С помощью модуля:
в) дать определение правильной и неправильной дроби 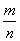 . .
г) записать фразу и пояснить её смысл: деталь признаётся бракованной, если её длина отличается от 20 сантиметров
больше, чем на полмиллиметра.
д) записать фразу и пояснить её смысл: максимально допустимая относительная погрешность прибора составляет 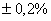 . .
Справка: относительная погрешность («дельта малая»): 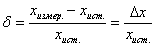 – это
отношение абсолютной погрешности к истинному значению величины. Если – это
отношение абсолютной погрешности к истинному значению величины. Если 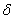 умножить на 100, то относительная погрешность будет выражена в процентах. умножить на 100, то относительная погрешность будет выражена в процентах.
Напоминаю, что эти задачи обязательны для выполнения – они являются неотъемлемой частью курса, поскольку в образцах
решения я рассказываю дополнительные и очень важные вещи по теме.
 2.8. Понятие системы 2.8. Понятие системы
 2.6. Метод интервалов 2.6. Метод интервалов
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики

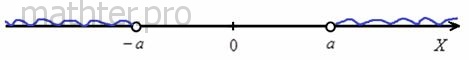
 2.8. Понятие системы
2.8. Понятие системы 2.6. Метод интервалов
2.6. Метод интервалов