2.6. Метод интервалов
Объяснять буду сразу на конкретном примере: 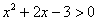 . Кстати, все ли до конца
понимают то, что нам предстоит сделать? Здесь нужно определить при каких «икс» квадратный трёхчлен
будет больше нуля. Итак, как решить это неравенство? . Кстати, все ли до конца
понимают то, что нам предстоит сделать? Здесь нужно определить при каких «икс» квадратный трёхчлен
будет больше нуля. Итак, как решить это неравенство?
На первом шаге нужно решить соответствующее уравнение, а также определить все недопустимые значения
«икс». Что касаемо недопустимых значений, то их здесь нет, поскольку квадратный трёхчлен 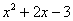 определён для всех «икс». А вот с розыском корней придётся потрудиться – решаем квадратное уравнение определён для всех «икс». А вот с розыском корней придётся потрудиться – решаем квадратное уравнение 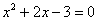 . .
Используя стандартный алгоритм, рассчитываем дискриминант:
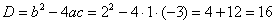 – отлично, извлекаем корень: – отлично, извлекаем корень:
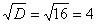 и находим сами корни: и находим сами корни:
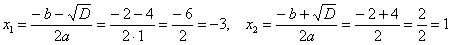
Не забываем о проверке! – мысленно подставляем значения 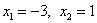 в уравнение в уравнение 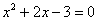 и
убеждаемся, что получаются верные равенства. и
убеждаемся, что получаются верные равенства.
На втором шаге отмечаем на числовой прямой все «нелегальные» точки и все корни. Поскольку наше неравенство строгое, то корни «выкалываем»:

Теперь нужно определить знаки, в нашем случае трёхчлена 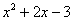 , на полученных интервалах. Как это сделать? Если квадратный трёхчлен больше (либо
меньше) нуля в какой-либо точке интервала, то он больше (либо меньше) нуля и во всех точках этого
интервала. В этом и состоит суть метода интервалов: , на полученных интервалах. Как это сделать? Если квадратный трёхчлен больше (либо
меньше) нуля в какой-либо точке интервала, то он больше (либо меньше) нуля и во всех точках этого
интервала. В этом и состоит суть метода интервалов:
1) Рассмотрим интервал 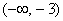 . Выберем любое значение,
принадлежащее этому интервалу, выгодно взять . Выберем любое значение,
принадлежащее этому интервалу, выгодно взять 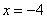 , и подставим его в
трёхчлен: , и подставим его в
трёхчлен:
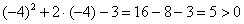 , значит трёхчлен больше нуля и во всех точках
этого интервала. , значит трёхчлен больше нуля и во всех точках
этого интервала.
2) Рассмотрим интервал 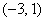 и подставим в трёхчлен наиболее удобное
значение и подставим в трёхчлен наиболее удобное
значение 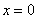 : : 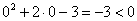 , значит, трёхчлен меньше нуля и во всех точках интервала. , значит, трёхчлен меньше нуля и во всех точках интервала.
3) И, наконец, интервал 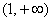 с подопытной точкой с подопытной точкой 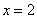 : :
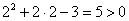 , значит, трёхчлен положителен и во всех
точках этого интервала. , значит, трёхчлен положителен и во всех
точках этого интервала.
Перечисленные подстановки выполняют устно, а результаты (полученные знаки) отмечают на чертеже. При этом нужные интервалы удобно
заштриховать:

Таким образом, решением неравенства являются два интервала, и ответ часто записывают в виде объединения промежутков: 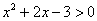 , если , если 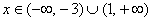
Используя метод интервалов, решим неравенство 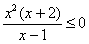 – здесь
нужно найти все значения «икс», при которых дробь будет меньше либо равна нулю. – здесь
нужно найти все значения «икс», при которых дробь будет меньше либо равна нулю.
Сначала определим недопустимые значения «икс» и корни соответствующего уравнения: 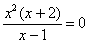 . И те и другие точки виднЫ невооружённым глазом: у нас есть нелегальное значение . И те и другие точки виднЫ невооружённым глазом: у нас есть нелегальное значение 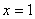 , которое обращает знаменатель в ноль, и корни , которое обращает знаменатель в ноль, и корни 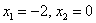 . Первую точку следует «выколоть», а вот корни «затушевать» – по той причине, что неравенство нестрогое: . Первую точку следует «выколоть», а вот корни «затушевать» – по той причине, что неравенство нестрогое:

Теперь определим знаки дроби 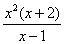 на полученных
интервалах: на полученных
интервалах:
1) Подставим значение 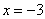 из интервала из интервала 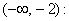
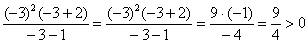 , значит, дробь больше нуля и во всех точках этого
интервала , значит, дробь больше нуля и во всех точках этого
интервала
2) Из интервала 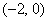 удобно выбрать значение удобно выбрать значение 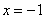 : :
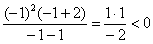 , значит, дробь меньше нуля и на всём
интервале. , значит, дробь меньше нуля и на всём
интервале.
3) Из интервала 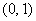 я выберу точку я выберу точку 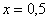 : :
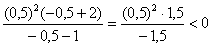 , значит, дробь отрицательна и на этом интервале. , значит, дробь отрицательна и на этом интервале.
4) И, наконец, из интервала 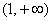 возьмём значение поменьше, а
именно возьмём значение поменьше, а
именно 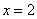 : :
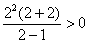 – заметьте, что для определения знака зачастую не
обязательно проводить вычисления или доводить их до конца. – заметьте, что для определения знака зачастую не
обязательно проводить вычисления или доводить их до конца.
Отмечаем на чертеже знаки и штрихуем нужные нам интервалы:

Ответ: 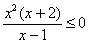 , если , если 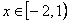
Что делать, если справа не ноль, а что-то другое? С помощью преобразований получить справа ноль :). Возможно, потребуется ещё «причесать» левую часть: привести дроби к общему знаменателю, привести подобные слагаемые и т.п.
А что делать, если нет ни «плохих» значений, ни корней? Тут всё просто – у нас один интервал (вся числовая прямая) и мы подставляем в
неравенство любое значение «икс». Если получено верное числовое неравенство, то решением является вся числовая прямая. Если
же получено неверное неравенство, то неравенство не имеет решений. Решим, например, неравенство 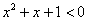 . У соответствующего уравнения . У соответствующего уравнения 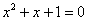 нет корней, поскольку дискриминант отрицателен: нет корней, поскольку дискриминант отрицателен: 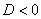 . И мы
просто подставляем в неравенство любое «икс», проще всего взять ноль: . И мы
просто подставляем в неравенство любое «икс», проще всего взять ноль:
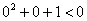
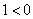 – в результате получено неверное числовое неравенство,
следовательно, неравенство – в результате получено неверное числовое неравенство,
следовательно, неравенство 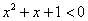 не имеет решений. не имеет решений.
Ну и легко понять, что решением неравенства 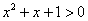 будет любое
«икс». будет любое
«икс».
Иногда из области рассмотрения следует исключить целые промежутки. Забегая вперёд, приведу неравенство с натуральным логарифмом: 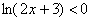 . «Начинка» любого логарифма строго положительна: . «Начинка» любого логарифма строго положительна: 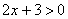 , а значит, нам нужно рассмотреть не всю числовую прямую, а лишь участок, где: , а значит, нам нужно рассмотреть не всю числовую прямую, а лишь участок, где: 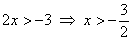 . Дорешаем позже! . Дорешаем позже!
 2.7. Уравнения и неравенства с модулем 2.7. Уравнения и неравенства с модулем
 2.5. Действия с неравенствами 2.5. Действия с неравенствами
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики



 2.7. Уравнения и неравенства с модулем
2.7. Уравнения и неравенства с модулем 2.5. Действия с неравенствами
2.5. Действия с неравенствами