3.5. Графическое решение уравнений и неравенств
В предыдущей главе мы решали уравнения и неравенства аналитически, и сейчас вдохнём в эти
задачи геометрический смысл. И это вас вдохновит! – это будет просто, это будет круто и это будет красиво! А, главное, чрезвычайно полезно.
Сначала частный случай. Чтобы решить уравнение вида 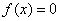 , нужно
построить график функции , нужно
построить график функции 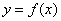 и посмотреть, где он пересекает ось
абсцисс. Там и находятся корни. Если точек пересечения нет, то уравнение не имеет действительных решений. и посмотреть, где он пересекает ось
абсцисс. Там и находятся корни. Если точек пересечения нет, то уравнение не имеет действительных решений.
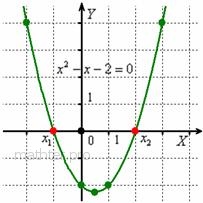 Так, при решении квадратного уравнения Так, при решении квадратного уравнения 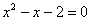 через
дискриминант мы получили корни через
дискриминант мы получили корни 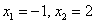 , но здесь можно просто построить
параболу, и всё понятно без комментариев. , но здесь можно просто построить
параболу, и всё понятно без комментариев.
Решением неравенства 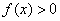 являются те промежутки, на которых график являются те промежутки, на которых график 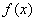 выше оси выше оси 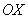 , ,
и, наоборот, 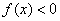 – там, где график – там, где график 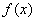 ниже оси. ниже оси.
Таким образом, вместо того, чтобы вымучивать неравенство 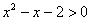 методом интервалов, просто смотрим на график и ответ готов: методом интервалов, просто смотрим на график и ответ готов: 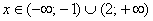 . .
Соответственно, решением неравенства 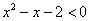 является интервал является интервал 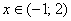 . .
В случае нестрогих неравенств 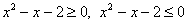 к решениям нужно добавить
пограничные точки: к решениям нужно добавить
пограничные точки: 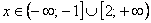 и и 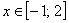 соответственно. соответственно.
А если вам не хочется возиться с нахождением опорных точек, «тыкая в них наугад» (ведь параболы бывают большие, размашистые), то есть общий случай:
Чтобы решить уравнение 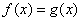 , нужно построить графики , нужно построить графики 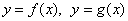 и найти их точки пересечения. «Иксовые» координаты этих точек и будут
решениями. Если графики не пересекаются, то действительных решений нет. и найти их точки пересечения. «Иксовые» координаты этих точек и будут
решениями. Если графики не пересекаются, то действительных решений нет.
Таким образом, вместо решения уравнения 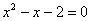 с вычерчиванием параболы,
представим его в виде с вычерчиванием параболы,
представим его в виде 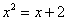 и изобразим элементарные графики: и изобразим элементарные графики:
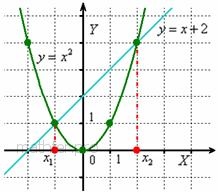 Подчёркиваю ещё раз, что решением являются «иксовые»
координаты точек пересечения. Подчёркиваю ещё раз, что решением являются «иксовые»
координаты точек пересечения.
Решением неравенства 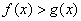 являются те промежутки, на которых график являются те промежутки, на которых график 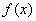 выше графика выше графика 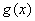 , и, наоборот: , и, наоборот: 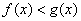 – там, где график – там, где график 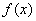 ниже графика ниже графика 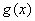 . .
Так, решением неравенства 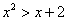 являются промежутки являются промежутки 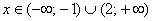 – поскольку на них парабола расположена выше прямой. И, наоборот, решением
неравенства – поскольку на них парабола расположена выше прямой. И, наоборот, решением
неравенства 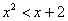 является промежуток является промежуток 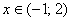 , так как здесь парабола расположена ниже прямой. Аналогично для нестрогих неравенств. , так как здесь парабола расположена ниже прямой. Аналогично для нестрогих неравенств.
Кстати, всем ли понятно, как из общих правил 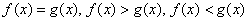 получаются частные
правила для получаются частные
правила для 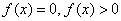 и и 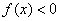 ? Элементарно. Это тот случай, когда ? Элементарно. Это тот случай, когда 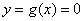 , а эта функция задаёт ось , а эта функция задаёт ось 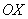 . .
Когда удобно использовать графический метод? Прежде всего, в простых случаях. Так, при решении неравенства 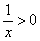 проще мысленно представить гиперболу, нежели использовать метод интервалов. Где гипербола выше оси проще мысленно представить гиперболу, нежели использовать метод интервалов. Где гипербола выше оси 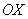 ? На интервале ? На интервале 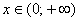 . Неравенству . Неравенству 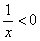 соответствует левая ветвь, которая лежит под осью, на
интервале соответствует левая ветвь, которая лежит под осью, на
интервале 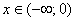 . И ещё этот метод хорош для лучшего понимания математики. . И ещё этот метод хорош для лучшего понимания математики.
Графический способ спасёт в экстремальных ситуациях, например, когда вы позабыли, как решать квадратное
уравнение, а помощи ждать неоткуда. Используйте приём, описанный выше – вместо уравнения 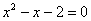 рассмотрИте рассмотрИте 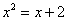 с двумя простыми
графиками, не построить которые – эт нужно постараться :) с двумя простыми
графиками, не построить которые – эт нужно постараться :)
Иногда графика эффективна в уравнениях «разнородными» функциями. Так, для решения уравнения 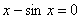 не существует стандартных аналитических методов, но это не беда. Мысленно представляем график не существует стандартных аналитических методов, но это не беда. Мысленно представляем график 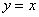 и график синуса и график синуса 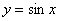 (о котором позже), после чего сразу понятно, что уравнение имеет единственный корень (о котором позже), после чего сразу понятно, что уравнение имеет единственный корень 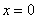 . .
Кстати, в некоторых задачах нужно просто определить количество корней и / или их приблизительное расположение, и на этот вопрос зачастую легко
ответит чертёж!
Разумеется, графики должны быть простыми – это важнейшее условие применения графического метода. Ибо строить 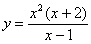 для решения для решения 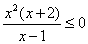 –
затея как-то не очень :) Уж лучше метод интервалов. –
затея как-то не очень :) Уж лучше метод интервалов.
И после этого невероятно полезного параграфа возвращается к нашим функциям:
 3.6. Показательная функция 3.6. Показательная функция
 3.4. СтепеннАя функция 3.4. СтепеннАя функция
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики Так, при решении
Так, при решении  Подчёркиваю ещё раз, что решением являются «иксовые»
координаты точек пересечения.
Подчёркиваю ещё раз, что решением являются «иксовые»
координаты точек пересечения. 3.6. Показательная функция
3.6. Показательная функция 3.4. СтепеннАя функция
3.4. СтепеннАя функция