3.6. Показательная функция
 Данная функция имеет вид Данная функция имеет вид 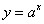 , где , где 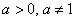 , при этом различают два
случая – когда основание находится в пределах , при этом различают два
случая – когда основание находится в пределах 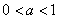 и когда и когда 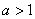 . Начнём со второго случая и в качестве примера рассмотрим мегапопулярную
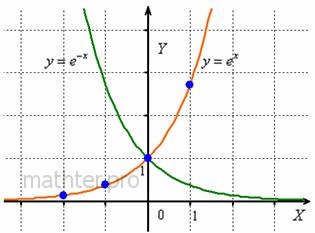
экспоненциальную функцию . Начнём со второго случая и в качестве примера рассмотрим мегапопулярную
экспоненциальную функцию 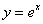 . .
Напоминаю, что 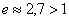 и для построения графика удобно выбрать следующие опорные
точки: и для построения графика удобно выбрать следующие опорные
точки:
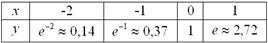
Наверняка вы слышали выражение «экспоненциальный рост». Это синоним роста в геометрической прогрессии –
он означает не просто быстрый, а «взрывной» рост. Уже при пяти получаем: 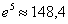 .
Таким образом, при увеличении «икс» график экспоненциальной функции круто взмывает вверх, а при уменьшении – бесконечно близко
приближается к своей асимптоте – оси .
Таким образом, при увеличении «икс» график экспоненциальной функции круто взмывает вверх, а при уменьшении – бесконечно близко
приближается к своей асимптоте – оси 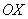 . Данная функция определена для всех «икс»: . Данная функция определена для всех «икс»: 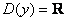 и строго
положительна: и строго
положительна: 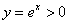 , то есть
полностью лежит над осью абсцисс. , то есть
полностью лежит над осью абсцисс.
Принципиально так же выглядят графики других показательных функций 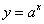 с основанием с основанием 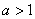 , например, , например, 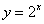 , , 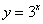 и др. Отличаться они будут крутизной. и др. Отличаться они будут крутизной.
График функции 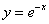 симметричен графику симметричен графику 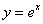 относительно оси относительно оси 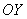 . .
И принципиально так же выглядит график любой показательной функции 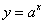 с основанием с основанием 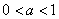 . .
На всякий случай: 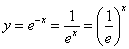 , т.е. основание функции равно , т.е. основание функции равно 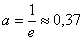 . .
Выражение «экспоненциальное убывание» означает убывание со стремительным ускорением. И в самом деле, возьмём ту же пятёрку: 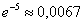 – почти уж у нуля. – почти уж у нуля.
Показательная функция не является чётной или нечётной (в обоих случаях), так как для неё не выполнено условие 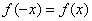 или или 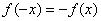 . .
И я вас поздравляю с экватором!
Где-то половина школьной программы пройдена! Может даже чуть больше.
И теперь они самые:
 3.7. Логарифмы и логарифмическая функция 3.7. Логарифмы и логарифмическая функция
 3.5. Графическое решение уравнений и неравенств 3.5. Графическое решение уравнений и неравенств
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики Данная функция имеет вид
Данная функция имеет вид  3.7. Логарифмы и логарифмическая функция
3.7. Логарифмы и логарифмическая функция 3.5. Графическое решение уравнений и неравенств
3.5. Графическое решение уравнений и неравенств