3.7. Логарифмы и логарифмическая функция
Оглавление:
Понятие логарифма
Свойства логарифмов
Логарифмирование и потенцирование
Логарифмическая функция и её график
Уравнения и неравенства с логарифмами
Понятие логарифма
Рассмотрим уравнение 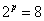 , которое задаёт нам вопрос: в какую степень нужно возвести 2, чтобы получить 8? На этот вопрос отвечает
логарифм , которое задаёт нам вопрос: в какую степень нужно возвести 2, чтобы получить 8? На этот вопрос отвечает
логарифм 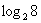 , который равен трём: , который равен трём: 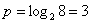 . …замысловато? Ну не зря же это проходят в старших классах :) . …замысловато? Ну не зря же это проходят в старших классах :)
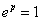 – в какую степень нужно возвести «е», чтобы получить 1? – в какую степень нужно возвести «е», чтобы получить 1? 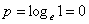
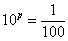 – в какую степень нужно возвести 10, чтобы получить 1/100? – в какую степень нужно возвести 10, чтобы получить 1/100? 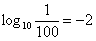
И вообще, 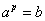 – в какую степень нужно возвести «а», чтобы получить
«бэ»? – в какую степень нужно возвести «а», чтобы получить
«бэ»?
Логарифмом числа 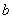 по основанию по основанию 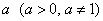 : :
– называется степень «пэ» 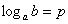 , в которую нужно возвести «а», чтобы получить «бэ». , в которую нужно возвести «а», чтобы получить «бэ».
Из чего следует основное логарифмическое тождество: 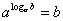 . .
…тождество – это такое железобетонное равенство :)
Сама запись 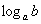 читается как « логарифм «бэ» по основанию «а»
», и очевидно, что логарифм определён лишь для положительных «бэ»: читается как « логарифм «бэ» по основанию «а»
», и очевидно, что логарифм определён лишь для положительных «бэ»: 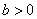 – по той причине, что положительное «а» в любой действительной степени «пэ»: – по той причине, что положительное «а» в любой действительной степени «пэ»: 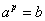 – положительно. – положительно.
Логарифм по основанию 10 называют десятичным логарифмом, и для краткости обозначают значком 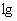 , например: , например: 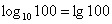 . .
Логарифм по основанию «е» называют натуральным логарифмом и обозначают значком 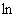 , например: , например: 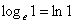 . В высшей математике
в ходу именно натуральные логарифмы, и в дальнейшем мы уделим им самое пристальное внимание. . В высшей математике
в ходу именно натуральные логарифмы, и в дальнейшем мы уделим им самое пристальное внимание.
Свойства логарифмов
Как и в случае со степенями / корнями, я не буду разбирать все свойства, а остановлюсь лишь на тех,
которые имеют большое значение для практики.
Переход к новому основанию: 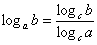 , причём новое
основание «цэ» вы можете выбрать по своему желанию (из доступных вариантов: , причём новое
основание «цэ» вы можете выбрать по своему желанию (из доступных вариантов: 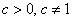 ), например: ), например:
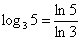 . Но гораздо чаще встречается частный случай формулы: . Но гораздо чаще встречается частный случай формулы: 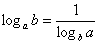 , например: , например: 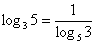 . Разумеется, формула работает и в обратном направлении, что бывает удобным, когда нужно избавиться от
знаменателя: . Разумеется, формула работает и в обратном направлении, что бывает удобным, когда нужно избавиться от
знаменателя: 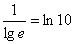 . .
Если 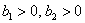 то справедливо следующее (и слева
направо и справа налево): то справедливо следующее (и слева
направо и справа налево):
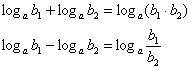
Например: 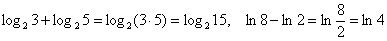 . .
Обращаю внимание, что эти действия выполнимы только для логарифмов с одинаковыми основаниями, не путайте с «похожими»
ситуациями: 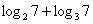 , , 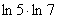 или или 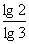 . Однако в последнем случае можно
сделать так: . Однако в последнем случае можно
сделать так: 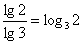 . .
Далее. Для 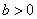 и любого действительного числа и любого действительного числа 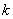 : :
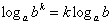
Например: 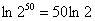 – и это просто волшебство! Ведь это здОрово избавиться от 50-й
степени! Популярно и обратное действие, особенно, когда нужно выполнить другие упрощения: – и это просто волшебство! Ведь это здОрово избавиться от 50-й
степени! Популярно и обратное действие, особенно, когда нужно выполнить другие упрощения: 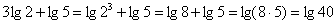
Перечисленные правила можно распространить на отрицательные значения «бэ», но тогда нужно добавить модули:
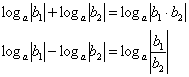
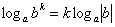 , если , если 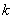 чётное. Например: чётное. Например: 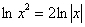 – и
равносильность соблюдена, поскольку полученный логарифм тоже определён для отрицательных «икс». – и
равносильность соблюдена, поскольку полученный логарифм тоже определён для отрицательных «икс».
А вот такое преобразование неравносильно: 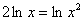 , и
поэтому здесь следует обязательно указать, что , и
поэтому здесь следует обязательно указать, что 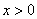 . .
В случае иных значений 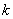 модуль не нужен: модуль не нужен: 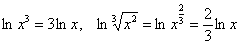 – по той причине, что и исходные и полученные логарифмы определены только для положительных
значений «икс». – по той причине, что и исходные и полученные логарифмы определены только для положительных
значений «икс».
Логарифмирование и потенцирование
Логарифмирование – это перевод чисел или уравнений в логарифмический масштаб или, попросту говоря, «навешивание» логарифмов.
Данное действие удобно использовать при работе с астрономическими или микроскопическими числами, особенно, если они находятся в произведении.
Так, число 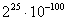 целесообразно уменьшить, «навесив» на него логарифм,
выгодно взять десятичный логарифм: целесообразно уменьшить, «навесив» на него логарифм,
выгодно взять десятичный логарифм: 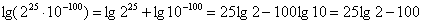 – далее переводим другие
числа в тот же масштаб (логарифмируем по основанию десять) – далее переводим другие
числа в тот же масштаб (логарифмируем по основанию десять)
и работаем (выполняем действия) с гораздо более маленькими значениями.
Логарифмирование незаменимо при решении некоторых уравнений, например:
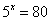
Для разрешения этого уравнения относительно «икс» «навесим» на обе его части логарифмы, обычно используют натуральные логарифмы:
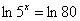
в левой части «сносим» степень, и порядок:
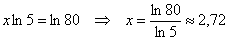
и «любительская» проверочка: 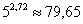 , около 80, что и требовалось проверить. , около 80, что и требовалось проверить.
При логарифмировании нужно следить за знаками, так, обе части уравнения (функции) 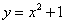 определены и положительны при любом значении «икс», поэтому здесь можно смело логарифмировать: определены и положительны при любом значении «икс», поэтому здесь можно смело логарифмировать: 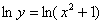 , получая равносильное уравнение. , получая равносильное уравнение.
А вот у функции 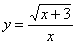 обе части могут быть меньше нуля, и поэтому здесь нужно
добавить модули: обе части могут быть меньше нуля, и поэтому здесь нужно
добавить модули: 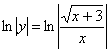 , квадратному корню модуль не нужен: , квадратному корню модуль не нужен: 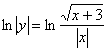 . Однако это действие всё равно неравносильно т.к. мы потеряли значение . Однако это действие всё равно неравносильно т.к. мы потеряли значение 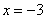 (почему?). Но это не помеха для решения некоторых задач, например, для
нахождения производной, где можно пренебречь даже модулями. Да, а зачем логарифмировать? Чтобы упростить правую часть: (почему?). Но это не помеха для решения некоторых задач, например, для
нахождения производной, где можно пренебречь даже модулями. Да, а зачем логарифмировать? Чтобы упростить правую часть: 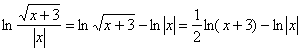 . .
Потенцирование – это обратная операция, «избавление» от логарифмов.
Предположим юные физики вдоволь нарезвились с вычислениями в десятичном логарифмическом масштабе, и хотят перевести результат 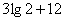 обратно. Без проблем: обратно. Без проблем:
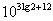 , используем свойства степеней, логарифмов и основное логарифмическое тождество: , используем свойства степеней, логарифмов и основное логарифмическое тождество: 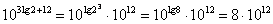 . .
Потенцирование используют для того, чтобы выразить функцию в явном виде, например: 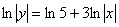 – «упаковываем» логарифмы в правой части: – «упаковываем» логарифмы в правой части:
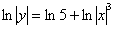
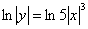 , после чего просто убираем логарифмы и модули заодно: , после чего просто убираем логарифмы и модули заодно:
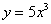
Такие действия выполняют при решении некоторых дифференциальных уравнений
Логарифмическая функция и её график
В логарифмической функции фиксируется основание «а», а значение «бэ» является независимой
переменной:
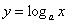 – данная функция каждому положительному значению «икс» ставит в
соответствие степень «игрек», такую, что: – данная функция каждому положительному значению «икс» ставит в
соответствие степень «игрек», такую, что: 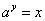
Таким образом, логарифмическая и показательная функция – это две взаимно обратные функции, и график
логарифма тоже представляет собой экспоненциальную кривую, только расположена она по-другому. Так, график натурального логарифма 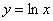 имеет следующий вид (запомните его!): имеет следующий вид (запомните его!):
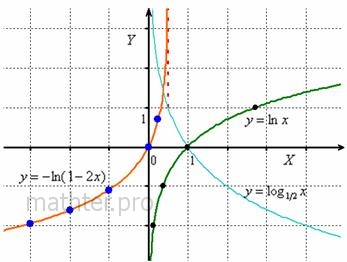 Удобные опорные точки: Удобные опорные точки:
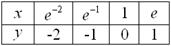
Принципиально так же выглядит график любого логарифма 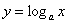 с основанием с основанием 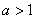 , в частности, десятичный логарифм , в частности, десятичный логарифм 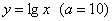
Если 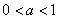 , то графики оказываются
«развёрнутыми наоборот» относительно оси , то графики оказываются
«развёрнутыми наоборот» относительно оси 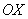 ,
например, ,
например, 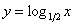 . Но такие логарифмы в высшей математике
встречаются довольно редко. . Но такие логарифмы в высшей математике
встречаются довольно редко.
Однако и в том и в другом случае логарифмическая функция 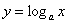 проходит
через точку проходит
через точку 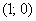 , а ось , а ось 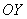 является вертикальной асимптотой графика. является вертикальной асимптотой графика.
Если «начинка» логарифма более сложная, то, естественно, график будет видоизменяться и мигрировать вместе с асимптотой. Построим, например,
график функции 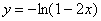 . Это удобно сделать по следующей
схеме: сначала из уравнения . Это удобно сделать по следующей
схеме: сначала из уравнения 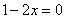 находим вертикальную асимптоту находим вертикальную асимптоту 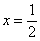 (оранжевый пунктир на чертеже). Теперь нужно выяснить область определения функции. Логарифм определён только в том случае, если его «начинка» строго больше нуля: (оранжевый пунктир на чертеже). Теперь нужно выяснить область определения функции. Логарифм определён только в том случае, если его «начинка» строго больше нуля: 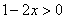 , и преобразуя это простое
неравенство, получаем, что: , и преобразуя это простое
неравенство, получаем, что: 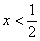 . Найдём затем несколько опорных точек: . Найдём затем несколько опорных точек:

и аккуратно соединим их линией. Для вычисления «игреков» удобно использовать калькулятор, например, Калькулятор,
приложенный к этой книге.
Ещё пример (на чертеже отсутствует): 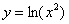 – график этого
логарифма имеет две симметричные относительно оси – график этого
логарифма имеет две симметричные относительно оси 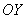 ветви (т.к. функция чётная), и эта функция не определена лишь в точке ветви (т.к. функция чётная), и эта функция не определена лишь в точке 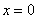 . А вот этот
логарифм: . А вот этот
логарифм: 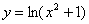 – определён всюду, поскольку – определён всюду, поскольку 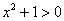 при любом значении «икс». при любом значении «икс».
Только что рассмотренные функции называют сложными или композиционными – это функции, в которые «вложены» другие функции: 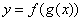 . В наших трёх примерах под логарифмом оказались линейная и квадратичные функции. . В наших трёх примерах под логарифмом оказались линейная и квадратичные функции.
Уравнения и неравенства с логарифмами
В параграфе о логарифмировании и потенцировании мы искусственно «навешивали» логарифмы на обе
части уравнения либо избавлялись от них. А сейчас речь пойдёт об уравнениях и неравенствах, где логарифм присутствует
изначально.
Начнем с простых случаев… и закончим ими:)
Уравнение вида 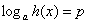 ( (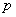 – константа) очевидным образом приводится к уравнению – константа) очевидным образом приводится к уравнению 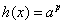 . Например: . Например:
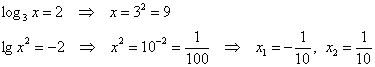
ну и давайте что-нибудь посодержательнее:
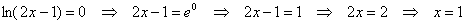
С геометрической точки зрения это означает, что график функции 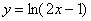 пересекает график пересекает график 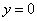 (ось (ось 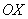 ) в точке ) в точке 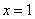 . .
И, конечно, проверка – подставим 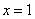 в левую часть
исходного уравнения: в левую часть
исходного уравнения:
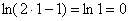 – в результате получена правая часть, ОК. – в результате получена правая часть, ОК.
Уравнение вида 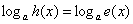 тоже разрешимо из естественных
соображений: логарифмы с одинаковыми основаниями равны, если тоже разрешимо из естественных
соображений: логарифмы с одинаковыми основаниями равны, если 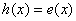 , при
этом корни должны быть ТАКИМИ, чтобы для них выполнялись условия , при
этом корни должны быть ТАКИМИ, чтобы для них выполнялись условия 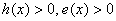 . Так, для
решения уравнения . Так, для
решения уравнения 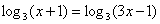 потенцируем обе части: потенцируем обе части:
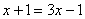 , откуда получаем корень , откуда получаем корень 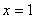 , после чего обязательно подставляем его в исходное уравнение: , после чего обязательно подставляем его в исходное уравнение: 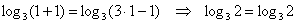 – верное равенство. – верное равенство.
А теперь рассмотрим такое уравнение: 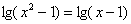 , где после избавления от
логарифмов всё вроде бы хорошо: , где после избавления от
логарифмов всё вроде бы хорошо: 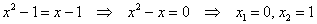 , однако корнями эти значения не
являются, т.к. не входят в область определения логарифмов. , однако корнями эти значения не
являются, т.к. не входят в область определения логарифмов.
Неравенства. Простейшие из них удобно решать графически, причём мысленно.
Рассмотрим неравенство 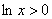 . Это неравенство предлагает нам определить участок,
где график натурального логарифма выше оси . Это неравенство предлагает нам определить участок,
где график натурального логарифма выше оси 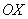 . Вспомнили, взглянули? . Вспомнили, взглянули? 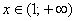 .
Аналогично, неравенству .
Аналогично, неравенству 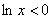 соответствует интервал соответствует интервал 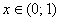 , где график логарифма ниже оси абсцисс. В случае нестрогих неравенств в
решения следует добавить единичку. , где график логарифма ниже оси абсцисс. В случае нестрогих неравенств в
решения следует добавить единичку.
И рассмотрим общий случай 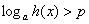 , где «пэ» – произвольная
константа. , где «пэ» – произвольная
константа.
Во-первых, «начинка» логарифма должны быть строго больше нуля: 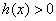 . Это незыблемое условие, о котором ни в коем случае забывать нельзя! Теперь разбираемся с
основным неравенством: сначала в правой части искусственно добавляем множитель: . Это незыблемое условие, о котором ни в коем случае забывать нельзя! Теперь разбираемся с
основным неравенством: сначала в правой части искусственно добавляем множитель: 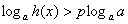 . Обратите внимание, что . Обратите внимание, что 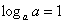 и статус-кво
соблюдён. В правой части поднимаем «пэ» в показатель: и статус-кво
соблюдён. В правой части поднимаем «пэ» в показатель: 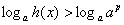 и дальше следует развилка: и дальше следует развилка:
если 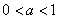 , то решаем систему , то решаем систему 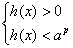 , если , если 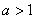 – то систему: – то систему: 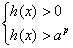 . .
Как видите, в 1-м случае после потенцирования знак неравенства следует
сменить на противоположный.
Неравенство 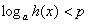 решается аналогично с финальными системами: решается аналогично с финальными системами:
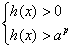 , если , если 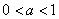 и и 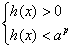 (без смены знака),
если (без смены знака),
если 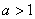 . .
Если изначальные неравенства нестрогие, то нижние неравенства в системах тоже будут нестрогими. И ещё раз –
условие 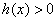 незыблемо при любых раскладах! незыблемо при любых раскладах!
Как я уже отмечал, на практике почти всегда встречает второй случай, когда 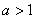 , ему и уделим внимание. Дорешаем неравенство , ему и уделим внимание. Дорешаем неравенство 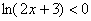 , которое мы начали в параграфе Метод интервалов. Там была найдена область
определения логарифма , которое мы начали в параграфе Метод интервалов. Там была найдена область
определения логарифма 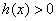 : :
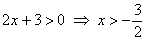 и сейчас нужно решить вторую часть задания. Согласно формальному
алгоритму, домножаем правую часть неравенства: и сейчас нужно решить вторую часть задания. Согласно формальному
алгоритму, домножаем правую часть неравенства: 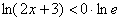 , поднимаем ноль наверх: , поднимаем ноль наверх:
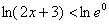 и получаем: и получаем: 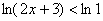 . Так как основание логарифма . Так как основание логарифма 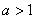 , то при
потенцировании знак неравенства менять не нужно: , то при
потенцировании знак неравенства менять не нужно: 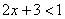 . Преобразуя это простенькое неравенство, получаем: . Преобразуя это простенькое неравенство, получаем: 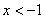 . Таким образом, имеем систему . Таким образом, имеем систему 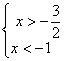 . Решение
1-го неравенства я отмечу сверху, а 2-го – снизу: . Решение
1-го неравенства я отмечу сверху, а 2-го – снизу:

Решением системы и исходного неравенства 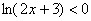 является
пересечение (общая часть) промежутков: является
пересечение (общая часть) промежутков: 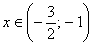 – да, вот такой вот совсем
небольшой интервал. – да, вот такой вот совсем
небольшой интервал.
Как вариант, неравенство 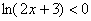 нетрудно решать графически – с графиком
этого логарифма никаких проблем. И я предлагаю вам это задание в числе других для самостоятельного выполнения. Если что-то не запомнилось или не
уложилось в голове, вернитесь к предыдущим параграфам: нетрудно решать графически – с графиком
этого логарифма никаких проблем. И я предлагаю вам это задание в числе других для самостоятельного выполнения. Если что-то не запомнилось или не
уложилось в голове, вернитесь к предыдущим параграфам:
Задание 8
а) Решить графически: 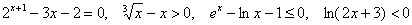
б) Определить количество действительных корней уравнения 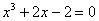
в) Почему уравнение 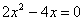 мы можем сократить на два, но на два нельзя сокращать правую часть мы можем сократить на два, но на два нельзя сокращать правую часть 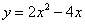 ? Пояснить аналитически и геометрически ? Пояснить аналитически и геометрически
г) Вычислить или упростить: 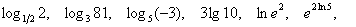
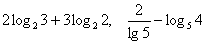 , пожалуй, хватит, а то уже извращение какое-то пошло :) , пожалуй, хватит, а то уже извращение какое-то пошло :)
д) Решить аналитически: 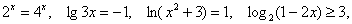
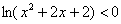 и для особых любителей пример посложнее: и для особых любителей пример посложнее: 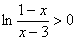 . .
Решения и ответы в конце книги.
 4.1. Геометрия. Элементарные геометрические фигуры 4.1. Геометрия. Элементарные геометрические фигуры
 3.6. Показательная функция 3.6. Показательная функция
| Оглавление |
|

 Кратчайший курс школьной математики
Кратчайший курс школьной математики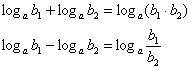
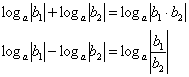
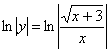 , квадратному корню модуль не нужен:
, квадратному корню модуль не нужен: 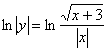 . Однако это действие всё равно неравносильно т.к. мы потеряли значение
. Однако это действие всё равно неравносильно т.к. мы потеряли значение 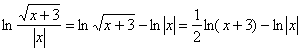 .
. Удобные опорные точки:
Удобные опорные точки: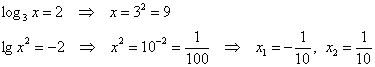
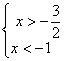 . Решение
1-го неравенства я отмечу сверху, а 2-го – снизу:
. Решение
1-го неравенства я отмечу сверху, а 2-го – снизу:
 4.1. Геометрия. Элементарные геометрические фигуры
4.1. Геометрия. Элементарные геометрические фигуры 3.6. Показательная функция
3.6. Показательная функция