|
Ваш репетитор, справочник и друг!
|
5.4. Как решить систему с помощью обратной матрицы?Для этого её нужно записать в матричной форме, которая элементарна: Убедимся в том, что эта запись корректна. Для этого выполним матричное умножение в левой части: Две матрицы равны, если равны их соответствующие элементы: Таким образом, корректность матричного уравнения Пример 102 Решить систему с матричным методом Решение: запишем систему в матричной форме: Решение найдем по формуле Обратную матрицу найдем по формуле Вычислим определитель матрицы коэффициентов, здесь я раскрыл определитель по первой строке: Если окажется, что Вычислим минор советующих элементов матрицы Таким образом: Теперь записываем обратную матрицу: Осталось выполнить матричное умножение. Обратите внимание, что деление на 60 выполняется в последнюю очередь. Всё разделилось красиво, и скорее всего мы не ошиблись. Но проверку лучше сделать привычкой и вот здесь можно потренироваться как раз в устном счёте. Ответ: Разумеется, решение может оказаться и дробным, и если вы подозреваете, что ошиблись, тем более выполните проверку! Или используйте Матричный калькулятор, в который я добавил довольно подробное решение этой задачи. Тренируемся самостоятельно: Пример 103 Решить систему с помощью обратной матрицы. Сверяемся с образцом и переходим к «королевскому» методу:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих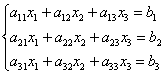 имеем:
имеем: 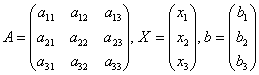 и получаем
и получаем 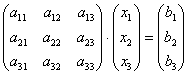
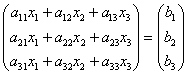
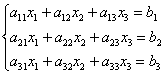
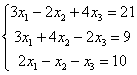
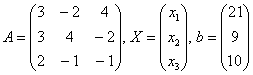
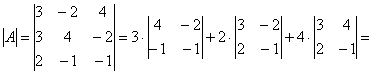
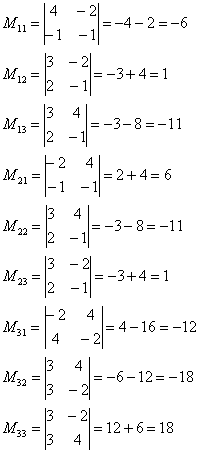
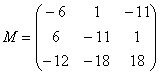 – матрица
– матрица 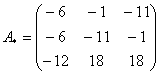 – матрица
– матрица 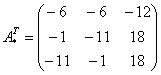 –
– 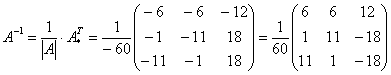
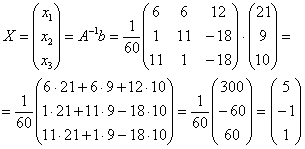
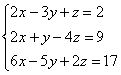
 5.5. Метод последовательного исключения неизвестных (Гаусса)
5.5. Метод последовательного исключения неизвестных (Гаусса) 5.3. Метод Крамера
5.3. Метод Крамера