|
Ваш репетитор, справочник и друг!
|
4.9. Матричные выраженияСначала повторим обычные выражения с числами. Числовое выражение состоит из чисел, знаков математических действий и скобок, например: При расчётах справедлив знакомый алгебраический приоритет: сначала учитываются скобки, затем выполняется возведение в степень / извлечение корней, потом умножение / деление и, наконец, в последнюю очередь – сложение /вычитание. Результат вычисления числового выражения является числом, например: Матричные выражения устроены практически так же! С тем отличием, что главными действующими лицами выступают матрицы. Плюс некоторые специфические матричные операции, такие, как транспонирование и нахождение обратной матрицы. Рассмотрим матричное выражение В первом слагаемом Во втором слагаемом С третьим слагаемым Что должно получиться в результате вычисления матричного выражения? Но если результат вычисления существует, то он тоже является матрицей. Как говорится, кошки не родят мышку. Это я о замкнутости алгебраической структуры относительно операций =) Следующие задания, как и все предыдущие, взяты из реальных практических работ, и мы начнём с самого простого: Пример 66 Даны матрицы Вычислить Решение: порядок действий очевиден, сначала выполняется умножение на число, затем сложение: Не удивляйтесь. Как я уже отмечал, заведомо невозможные действия часто предлагаются в заданиях данного типа. Пробуем вычислить второе выражение: Тут всё нормально. Ответ: действие Чуть повысим сложность: Пример 67 Даны матрицы Решать во многих случаях (но не всегда) лучше по порядку, и мы начинаем с произведения А вот с произведением Здесь на первом же шаге множитель (–1) удобно вынести вперёд, чтобы разобраться с ним в самую последнюю очередь. Но вот если бы в матрице С более сложными выражениями вроде Сначала находим произведение: Более подготовленные читатели могут оформить решение «одной строкой»: Ответ: действие Задание: для матриц Примера 67 выполнить действия Образец для сверки в конце книги. И ещё один пример – тренировки много не бывает: Пример 68 Вычислить значение матричного многочлена Здесь решение удобно оформить по пунктам. Образец в конце книги. Теперь вы знаете достаточно много действий с матрицами, чтобы освоить «высшее» матричное образование:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих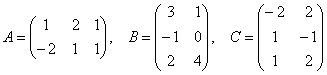 .
.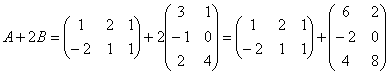
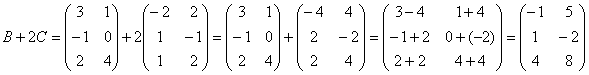
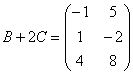 .
.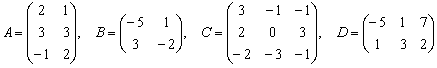 . Найти значения следующих выражений:
. Найти значения следующих выражений: 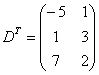 и далее
и далее 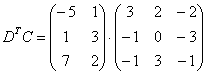 , которое выполнить нельзя, так как число столбцов матрицы
, которое выполнить нельзя, так как число столбцов матрицы 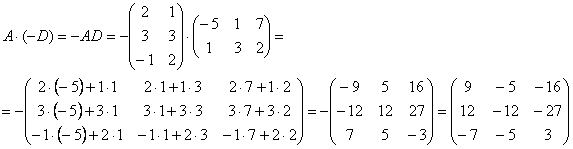
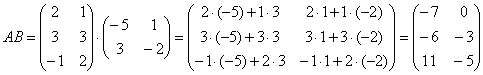
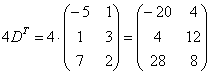
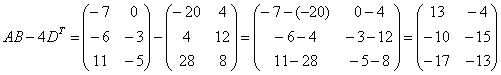
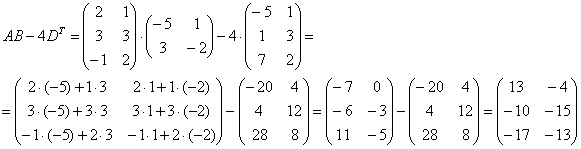
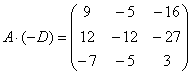 ,
, 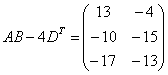 .
. 4.10. Матрицы с точки зрения алгебраической структуры
4.10. Матрицы с точки зрения алгебраической структуры 4.8.4. Как возвести матрицу в куб и более высокие степени?
4.8.4. Как возвести матрицу в куб и более высокие степени?