|
Ваш репетитор, справочник и друг!
|
5.6. Несовместные системыРазберём особенности этого случая в конкретных задачах: Пример 109 Решить систему линейных уравнений Что сразу бросается в глаза в этой системе? Количество уравнений – оно меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных, то можно сразу сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить безотказным методом Гаусса. Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Сами элементарные преобразования – точно такие же, разница будет в концовке решения: Ну и, наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: Если в результате элементарных преобразований получена строка вида Как записать концовку задания? Можно так и записать: «в результате элементарных преобразований получена строка вида Разумеется, здесь нет никакого обратного хода алгоритма Гаусса, по той причине, что решения отсутствуют, и находить попросту нечего. Тренируемся самостоятельно: Пример 110 Решить систему уравнений Несмотря на то, что система имеет «правильный» формат (количество уравнений равно количеству неизвестных), это ещё ничего не значит. Тут возможны все варианты: либо решений нет, либо оно единственно, либо их бесконечно много. Условие не требует от нас использовать какой-то конкретный метод решения, и в таких ситуациях, конечно же, лучше применить метод Гаусса. Свериться с образцом можно в конце книги. И вновь напомню, что ваш ход решения может отличаться от моего, ибо у алгоритма Гаусса нет «жёсткости». Ещё одна техническая особенность решения состоит в том, что элементарные преобразования можно прекращать сразу же, как только появилась строка вида Однако существует более строгое обоснование совместности / несовместности системы, и если того требует условие задачи и / или Ваш рецензент, то решение следует оформить в более солидном ключе:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих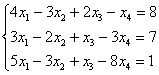
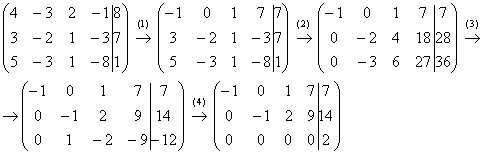
 обратно в систему:
обратно в систему: 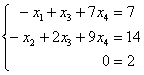 . Нижняя строка представляет собой неверное числовое равенство, что сигнализирует о несовместности системы.
. Нижняя строка представляет собой неверное числовое равенство, что сигнализирует о несовместности системы.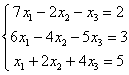
 . Матрица ещё не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет надобности, так как появилась строка вида
. Матрица ещё не приведена к ступенчатому виду, но в дальнейших элементарных преобразованиях нет надобности, так как появилась строка вида  5.7. Как исследовать систему линейных уравнений на совместность?
5.7. Как исследовать систему линейных уравнений на совместность? 5.5. Метод последовательного исключения неизвестных (Гаусса)
5.5. Метод последовательного исключения неизвестных (Гаусса)