|
Ваш репетитор, справочник и друг!
|
5.7. Как исследовать систему линейных уравнений на совместность?Как правило, с помощью теоремы Кронекера-Капелли: система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её матрицы системы равен рангу расширенной матрицы системы: Следствие: совместная система имеет единственное решение, если Посмотрим, как это работает на практике: Пример 111 Исследовать систему на совместность и найти её решение, если система совместна Не тушуйтесь, системы а) и б) уже прорешаны! Но тут есть дополнительное задание: исследовать систему на совместность. Поскольку в условии не предложен способ решения, то, разумеется, используем метод Гаусса. И не только по причине его универсальности. Ступенчатый вид расширенной матрицы системы автоматически сообщит нам ранги, в результате чего мы легко воспользуемся теоремой Кронекера-Капелли и сделаем вывод о совместности либо несовместности системы. Решение: а) Это система из Примера 104, которая уже приведена к ступенчатому виду: Поскольку элементарные преобразования не меняют ранг матрицы, то в результате этих действий получены эквивалентная исходной матрица системы Обе матрицы имеют ступенчатый вид, причём в каждой матрице три стоки, следовательно, вывод таков: Дальше раскручиваем обратный ход метода Гаусса и записываем ответ, что уже также выполнено в Примере 104. б) Вторую систему я взял из Примера 109, и финальная матрица тоже известна: В результате элементарных преобразований получена эквивалентная исходной матрица системы Приведём матрицу системы к ступенчатому виду, удалив нулевую строку: Количество строк ступенчатой матрицы равно двум, поэтому Расширенная же матрица системы имеет готовый ступенчатый вид и количество её строк равно трём, следовательно, Вывод: Следует заметить, что обоснование этого факта можно провести и через миноры: Максимальный порядок ненулевого минора матрицы системы равен двум, например: Максимальный порядок ненулевого минора расширенной матрицы системы равен трём, например: Вывод такой же, и эта версия тоже встречается в некоторых методичках.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих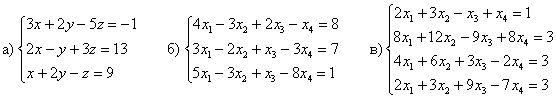
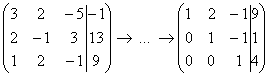 .
.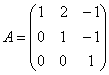 и
и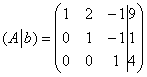 .
.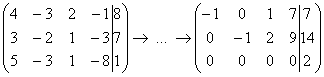
 и расширенная матрица
и расширенная матрица 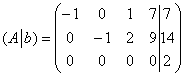 .
.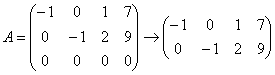
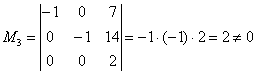 , таким образом,
, таким образом,  5.8. Системы с бесконечным количеством решений
5.8. Системы с бесконечным количеством решений 5.6. Несовместные системы
5.6. Несовместные системы