|
Ваш репетитор, справочник и друг!
|
5.8. Системы с бесконечным количеством решений– очень частый гость на практике, наряду со случаем единственного решения. И в качестве иллюстрации сразу решим систему под пунктом «в» (Пример 111): На первый взгляд тут всё «стандартно» (4 уравнения и 4 неизвестные), но это не даёт нам никакой информации о совместности системы и количестве решений. Используем метод Гаусса. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: В результате элементарных преобразований получена эквивалентная исходной матрица системы Обе матрицы имеют ступенчатый вид и в каждой из них две строки. Вывод: Осталось только найти это множество решений. Не откажем себе в удовольствии выделить простым карандашом «лестницу» и «ступеньки» полученной матрицы: Бесконечное множество решений коротко записывают в виде так называемого общего решения системы. Как найти общее решение? С помощью того же обратного хода метода Гаусса, правда, с некоторой спецификой Сначала нужно определить, какие переменные у нас являются базисными, а какие переменные – свободными. Базисные переменные «сидят» на ступеньках матрицы. А посему базисными являются переменные Свободные переменные – это все оставшиеся переменные, которым не досталось ступеньки. В нашем случае их две: Теперь нужно ВСЕ базисные переменные выразить только через свободные переменные. Обратный ход алгоритма Гаусса традиционно работает снизу вверх: Как правильно записать общее решение? Свободные переменные записываются в общее решение «сами по себе» и строго на своих местах. В данном случае свободные переменные Из общего решения системы можно найти бесконечно много частных решений. Это очень просто. Дело в том, что свободным переменным, в нашем примере Подставим Другая сладкая парочка – единицы, подставим Легко понять, что система имеет бесконечно много частных решений, а это значит, что каждое частное решение удовлетворяет каждому уравнению системы. На этом основана «быстрая» проверка правильности решения. Возьмите, например, частное решение …Есть? Всё должно сойтись. И с любым полученным частным решением – тоже всё должно сойтись. Но это всё-таки не внушает доверия. Более основательна и надёжна проверка общего решения. Как проверить полученное общее решение Это несложно, но довольно муторно. Нужно взять выражения базисных переменных, в данном случае Кроме того, в некоторых заданиях требуют проверку общего решения: Пример 112 Решить систему методом Гаусса. Найти общее решение и два частных. Сделать проверку общего решения. Это пример для самостоятельного решения. И еще пара задач для отработки алгоритмов, не пропускаем! Пример 113 Доказать, что система совместна и имеет бесконечно много решений. Записать общее решение и два частных. Выполнить проверку. Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду: В результате преобразований получена эквивалентная исходной матрица системы Обе матрицы имеют ступенчатый вид и три строки, Выполним пометки карандашом: Запишем для удобства ступенчатую систему: Из третьего уравнения: Рассмотрим первое уравнение В ходе вычислений удобно использовать Калькулятор обыкновенных дробей, который я на всякий случай тоже приложил к книге. Итак, общее решение: Ещё раз, как оно получилось? Свободная переменная Сразу выполним проверку общего решения. Работа для негров, но она у меня уже выполнена, поэтому ловите =) Подставляем трофеи В результате получены правые части соответствующих уравнений, таким образом, общее решение найдено правильно. Теперь из найденного общего решения Ответ: система совместна по теореме Кронекера-Капелли, общее решение: Отрабатываем технику вычислений: Пример 114 Решить систему линейных уравнений. Обратите внимание, что условие сформулировано максимально свободно, выбор метода решения – это ваш выбор, и проверять / не проверять – тоже ваш ;) …Зря я тут про негров вспомнил, теперь в голову полезли всякие садистские мотивы, и вспомнилась фотожаба, где куклуксклановцы в белых балахонах бегут по футбольному полю за чернокожим футболистом. Сижу, тихо улыбаюсь. Знаете, как отвлекает…. Остановлюсь на некоторых особенностях решения, которые не встретились в недавних примерах. В общее решение системы иногда может входить константа (или константы), например: Редко, но встречаются системы, в которых количество уравнений больше количества переменных. Метод Гаусса работает в самых суровых условиях, следует невозмутимо привести расширенную матрицу системы к ступенчатому виду по стандартному алгоритму. Такая система может быть несовместной, может иметь бесконечно много решений, и… может иметь единственное решение! Снабдим систему с единственным решением Да, ещё стандартные сокращения, совсем забыл, они в ходу не только в алгебре: о / р – общее решение, ч / р – частное решение. Теперь познакомимся с достаточно популярным частным случаем СЛУ:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
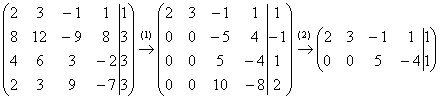
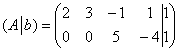 .
.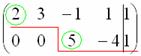 ,
,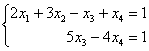
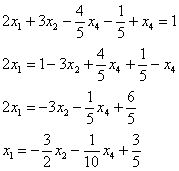
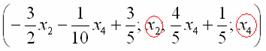 .
.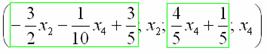
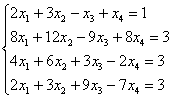
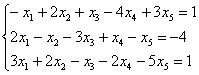
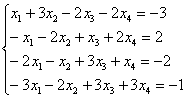
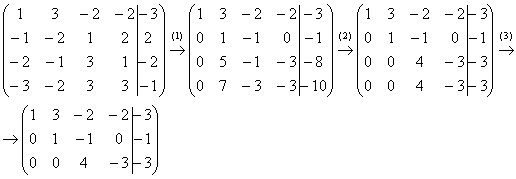
 и расширенная матрица системы
и расширенная матрица системы  .
. 
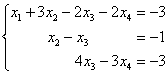
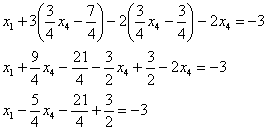
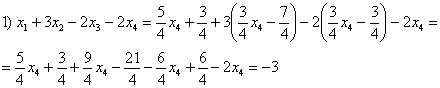
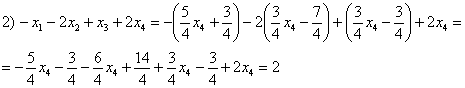
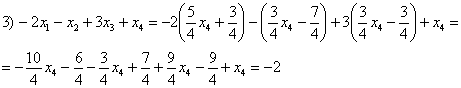
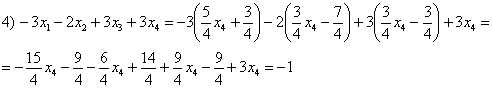
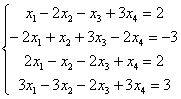
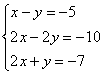 .
. 5.9. Однородные системы линейных уравнений
5.9. Однородные системы линейных уравнений 5.7. Как исследовать систему линейных уравнений на совместность?
5.7. Как исследовать систему линейных уравнений на совместность?