|
Ваш репетитор, справочник и друг!
|
5.9. Однородные системы линейных уравненийСистема линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например: Совершенно понятно, что однородная система всегда совместна, то есть всегда имеет решение. …А всем ли, кстати, совершенно, и всем ли понятно? Прежде всего, в глаза бросается тривиальное решение Пример 115 Решить однородную систему линейных уравнений Решение: используем метод Гаусса. Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Обратите внимание, что здесь не имеет смысла рисовать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями: В результате элементарных преобразований получена эквивалентная однородная система ответ: Повторяем самостоятельно: Пример 116 Решить однородную систему линейных уравнений В обоих примерах ранг матрицы системы (три) равен количеству переменных ( Пример 117 Решить однородную систему линейных уравнений Решение: как мы видим, тривиальное решение никуда не убежало, однако есть ли решения ещё? Запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду. Первое действие (1) направлено не только на получение единичного значения слева вверху, но и на уменьшение чисел в матрице – это ещё один технический приём, который реально спасает: В результате элементарных преобразований получена эквивалентная система: Выразим базисные переменные через свободную переменную: Ответ: общее решение: Нулевое решение входит в общую формулу при Проверка выполняется по обычной схеме: полученное общее решение нужно подставить в левую часть каждого уравнения системы, тут это просто и приятно: И на этом можно было бы тихо-мирно закончить, но решение однородной системы уравнений часто требуется представить в векторной форме, с помощью так называемой фундаментальной системы решений.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих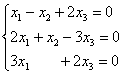
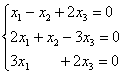
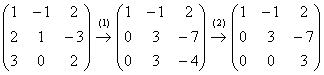
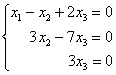 , и, применяя обратный ход метода Гаусса, можно сразу записать
, и, применяя обратный ход метода Гаусса, можно сразу записать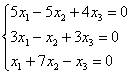
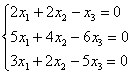
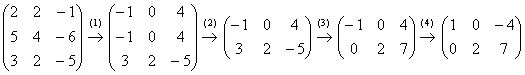
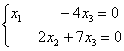 и обратный ход работает
и обратный ход работает 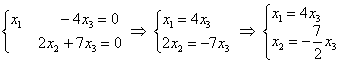
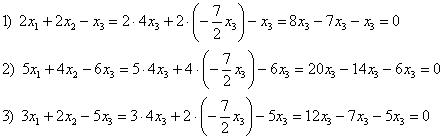
 5.9.1. Фундаментальная система решений однородной системы
5.9.1. Фундаментальная система решений однородной системы 5.8. Системы с бесконечным количеством решений
5.8. Системы с бесконечным количеством решений