Ваш репетитор, справочник и друг!

Высшая алгебра для начинающих

5.9.1. Фундаментальная система решений однородной системы

Пожалуйста, забудьте о геометрии, поскольку сейчас речь пойдёт о векторах в их общем алгебраическом смысле, к которому мы почти подобрались…. Ничего страшного, если что-то покажется не очень понятным, скоро во всём разберёмся!

Фундаментальная система решений – это множество линейно независимых векторов , каждый из которых является решением однородной системы. Кроме того, решением также является любая линейная комбинация данных векторов: , где – произвольные действительные числа.

Количество векторов фундаментальной системы рассчитывается по формуле:
.

Однако в практических задачах гораздо удобнее ориентироваться на следующий признак: количество векторов фундаментальной системы равно количеству свободных неизвестных.

Представим общее решение только что решённой системы в векторной форме. Свободная переменная в данном случае одна, поэтому фундаментальная система решений состоит из единственного вектора . Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать и получить: . Координаты вектора удовлетворяют каждому уравнению системы.

Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из единственного слагаемого. Общее решение однородной системы обозначим через вектор (подстрочный индекс расшифровывается «общее однородной»):
общее решение: , где (любое вещественное число)

Это так называемый нормальный способ построения фундаментальной системы – когда свободным переменным придаются исключительно единичные значения.

Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому можно взять и из общего решения получить вектор с целыми координатами: .

Тогда ответ запишется в эквивалентной форме:
, где (любое вещественное число).

Оба варианта ответа корректны, однако «чайникам» я всё-таки рекомендую классику жанра – нормальность (единичные значения свободных переменных).
Придавая параметру различные действительные значения, можно получить бесконечно много частных решений. Возьмём нормальное решение и, например, значение . Тогда вектор соответствующего частного решения таков:
(ЧO – «частное решение однородной системы)

И я доверяю Вам более масштабную систему:

Пример 118

Решить однородную систему линейных уравнений

Ответ записать с помощью фундаментальной системы решений.

Разумеется, ф / с может содержать бОльшее количество векторов:

Пример 119

Найти общее решение однородного уравнения и записать ответ в векторной форме

Решение: запишем матрицу системы и с помощью элементарных преобразований приведём ее к ступенчатому виду:

(1) Сначала получим единичное значение на 1-й «ступеньке». Перестановкой строк это не решить, а посему к первой строке прибавим третью строку, умноженную на –1.
(2) Ко второй, третьей и четвертой строкам прибавили первую строку, умноженную на 5, 4 и 5 соответственно. Ещё раз оценИте, как удобна именно «минус» единица!
(3) Последние три строки пропорциональны, оставляем лишь одну из них. У первой строки меняем знак.
(4) А почему бы нет? К первой строке прибавим вторую, умноженную на –1.

Понятно, что – базисные переменные, – свободные переменные, и мы получаем вот такую вот стильную картину:

Таким образом, общее решение: .

Не забываем о проверке! – для этого нужно подставить выражения базисных переменных в левую часть каждого уравнения системы и в результате тотальных сокращений получить нули.

Найдем векторы фундаментальной системы решений. Для этого последовательно выбираем напрашивающиеся пары значений свободных переменных:
если , то ;
если , то

Обращаю внимание, что векторы фундаментальной системы линейно независимы, поэтому нас устраивают далеко не все пары значений. А именно, не годятся пропорциональные пары, например, и или и , поскольку с ними мы получим пропорциональные (линейно зависимые) векторы.

Ответ: общее решение: , где – произвольные действительные числа.

Теперь коснёмся следующего интересного вопроса:

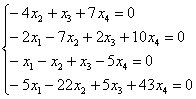
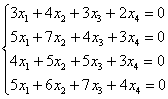
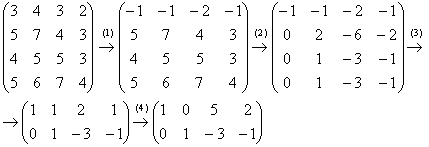
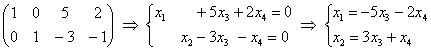
5.9.2. Выбор базисных переменных

5.9. Однородные системы линейных уравнений

| Оглавление |

Автор: Aлeксaндр Eмeлин