|
Ваш репетитор, справочник и друг!
|
5.9.2. Выбор базисных переменныхДо сих пор в качестве базисных переменных мы выбирали те, которые «сидят на ступеньках». Так, в горячем примере была получена ступенчатая матрица И возникает вопрос: это единственный вариант? Нет! Чем, собственно, хуже «перевёрнутая лестница»? Давайте к первой строке прибавим вторую: Таким образом, Проверьте, что Но ещё более приятная картинка получится, если мы запишем систему: …Так что же мешает выбрать в качестве базисных переменные Таким образом, общее решение: Немного поколдовав над матрицей, можно выразить иные пары базисных переменных, всего здесь будет 6 вариантов. И практический ориентир выбора базисной переменной таков: если в столбце матрицы системы находятся нули, за исключением одной ячейки, то соответствующую переменную можно выбрать в качестве базисной, при условии, что в строке с ненулевой ячейкой ещё не выбрана базисная переменная. Однако практика не всегда щедрА на подарки, поэтому надёжнее придерживаться стандартных «ступенек», особенно, если Вы новичок. Самостоятельно: Пример 120 Решить однородную систему, ответ записать в векторной форме. В образце решения я применил стандартный алгоритм. Здесь фундаментальная система содержит три вектора, которые проще всего найти, используя следующие тройки значений свободных переменных: И пара творческих заданий: Очевидно, принципы выбора базисных переменных справедливы не только для однородных, но и для «обычных» неоднородных систем с общим решением. Между которыми что-то, да должно ещё быть….
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих
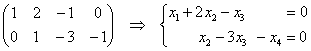
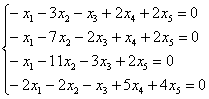
 5.9.3. Взаимосвязь решений неоднородной и однородной системы
5.9.3. Взаимосвязь решений неоднородной и однородной системы 5.9.1. Фундаментальная система решений однородной системы
5.9.1. Фундаментальная система решений однородной системы