5.9.3. Взаимосвязь решений неоднородной и однородной системы
Представьте двух близких родственниц: неоднородную систему (у которой хотя бы один свободный член отличен от нуля) и такую же систему – только с нулевыми свободными членами (то бишь, соответствующую однородную систему).
Логично предположить, что если системы отличаются лишь столбцом свободных членов, то между их решениями должна существовать тесная связь. … И это действительно так! Всё разберём в конкретном примере:
Пример 121
Дана система линейных уравнений
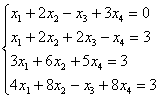
Требуется:
1) найти общее решение;
2) используя результат предыдущего пункта, найти общее решение соответствующей однородной системы и записать его в векторной форме.
…Страха я тут нагнал во втором пункте, но мы его преодолеем :)
Решение: по условию, дана «обычная» неоднородная система уравнений, и первая часть не отличается новизной:
1) Запишем расширенную матрицу системы (не зеваем нолик в третьей строке) и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на –3. К четвёртой строке прибавили первую строку, умноженную на –4.
(2) Последние три строки одинаковы, две из них удалили.
Обратный ход:
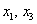 – базисные переменные (они расположены на «ступеньках»); – базисные переменные (они расположены на «ступеньках»);
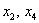 – свободные переменные (которым «ступеньки» не досталось). – свободные переменные (которым «ступеньки» не досталось).
Выразим базисные переменные через свободные. Из 2-го уравнения 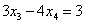 выразим выразим 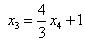 и подставим в 1-е уравнение и подставим в 1-е уравнение 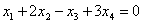 : :
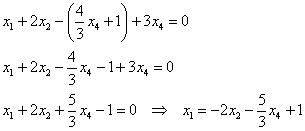
Общее решение неоднородной системы обозначим через 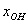 . .
Ответ: 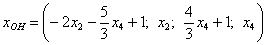
2) Во второй части задания требуется найти общее решение 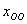 такой же, только однородной системы такой же, только однородной системы 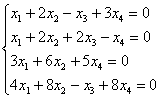 , причём, по условию, необходимо использовать ответ предыдущего пункта. Выполнять элементарные преобразования заново, как вы правильно догадались, не нужно. , причём, по условию, необходимо использовать ответ предыдущего пункта. Выполнять элементарные преобразования заново, как вы правильно догадались, не нужно.
Правило: общее решение неоднородной системы 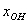 равно сумме общего решения соответствующей однородной системы равно сумме общего решения соответствующей однородной системы 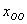 и какого-либо (любого!) частного решения неоднородной системы и какого-либо (любого!) частного решения неоднородной системы 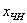 : :
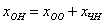
Откуда легко выражается общее решение нашей однородной системы:
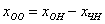
Общее решение неоднородной системы найдено в первом пункте:
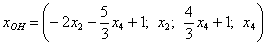 , и осталось найти какое-нибудь частное решение , и осталось найти какое-нибудь частное решение 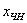 . Проще всего взять нулевые значения свободных переменных . Проще всего взять нулевые значения свободных переменных 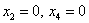 : :
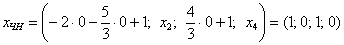
Таким образом, общее решение соответствующей однородной системы:
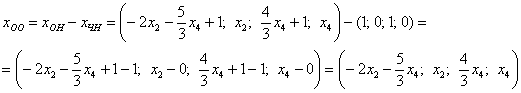
Задание: самостоятельно проверьте найденное решение, подставив 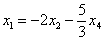 и и 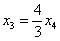 в левую часть каждого уравнения однородной системы. в левую часть каждого уравнения однородной системы.
Представим 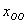 в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений состоит из двух векторов. Пойдём классическим путём, с некоторой, впрочем, поправкой: в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений состоит из двух векторов. Пойдём классическим путём, с некоторой, впрочем, поправкой:
рассмотрим пару значений свободных переменных 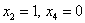 и получим первый вектор: и получим первый вектор: 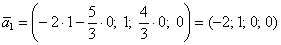 – координаты данного вектора удовлетворяют каждому уравнению однородной системы (проверьте устно!). – координаты данного вектора удовлетворяют каждому уравнению однородной системы (проверьте устно!).
Теперь вторая «стандартная» пара: 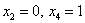 …, но хорошА ли она? Если её подставить в общее решение …, но хорошА ли она? Если её подставить в общее решение 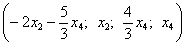 , то получатся дроби. А оно зачем? , то получатся дроби. А оно зачем?
Поэтому здесь удобнее взять пропорциональные значения 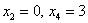 , чтобы получить целые координаты второго вектора: , чтобы получить целые координаты второго вектора: 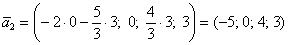 – этот вектор тоже удовлетворяют каждому уравнению однородной системы (проверьте!). – этот вектор тоже удовлетворяют каждому уравнению однородной системы (проверьте!).
И вообще, произвольная линейная комбинация векторов фундаментальной системы 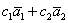 , где , где 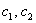 – любые действительные числа, является решением данной системы, – любые действительные числа, является решением данной системы,
ответ: 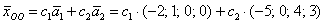 , где , где 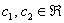
Иными словами, если взять два любых вещественных числа, скажем, 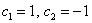 , то получится вектор частного решения однородной системы: , то получится вектор частного решения однородной системы:
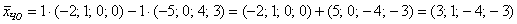
…Порядком я, наверное, Вас подзапутал, поэтому перечитайте задание еще раз :). И тогда из правила 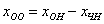 окончательно станет понятной следующая вещь: поскольку частное решение окончательно станет понятной следующая вещь: поскольку частное решение 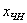 мы можем взять любое, то общее решение однородной системы мы можем взять любое, то общее решение однородной системы 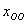 запишется бесконечным количеством способов, и понятно, все они будут эквивалентны друг другу. Вот такое вот многоликое общее решение! запишется бесконечным количеством способов, и понятно, все они будут эквивалентны друг другу. Вот такое вот многоликое общее решение!
 5.10. Метод Гаусса-Йордана 5.10. Метод Гаусса-Йордана
 5.9.2. Выбор базисных переменных 5.9.2. Выбор базисных переменных
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих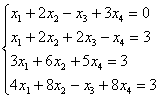

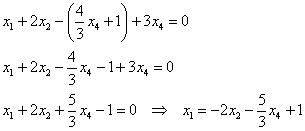
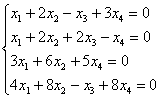 , причём, по условию, необходимо использовать ответ предыдущего пункта. Выполнять элементарные преобразования заново, как вы правильно догадались, не нужно.
, причём, по условию, необходимо использовать ответ предыдущего пункта. Выполнять элементарные преобразования заново, как вы правильно догадались, не нужно.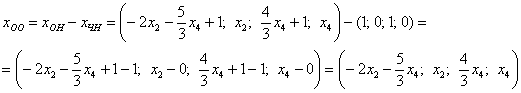
 5.10. Метод Гаусса-Йордана
5.10. Метод Гаусса-Йордана 5.9.2. Выбор базисных переменных
5.9.2. Выбор базисных переменных