|
Ваш репетитор, справочник и друг!
|
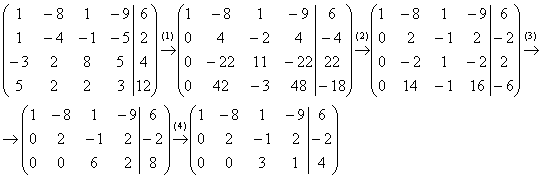
5.10. Метод Гаусса-ЙорданаИли метод Гаусса-Жордана – в русскоязычных источниках повелось неверно транскрибировать фамилию Jordan немецкого математика Вильгельма Йордана. Элементы этого метода я уже начал применять в предыдущих параграфах, и сейчас пришло расставить все точки над «J» :) В ходе использования метода Гаусса мы приводили матрицу к ступенчатому виду следующим образом: Но возникает вопрос, а почему бы её не привести так: Этот способ совершенно равноценен и может быть неудобен только по причине субъективного восприятия. Однако чего тут мелочиться? – подумал немец Йордан и предложил сразу привести её к виду Возможно ли это? Да, возможно! Так давайте воплотим эту замечательную идею в жизнь! – повторив путь немецкого математика. Как Вы правильно догадываетесь, метод Гаусса-Йордана представляет собой модификацию метода Гаусса: Пример 122 Решить систему методом Гаусса-Йордана Это система из Примера 104 и начало решения такое же. Запишем расширенную матрицу системы и с помощью элементарных преобразований (у нас там получилось 5 шагов) приведём её к ступенчатому виду: Но теперь вместо обратного хода в игру вступают дополнительные элементарные преобразования. Сначала нам нужно получить нули вот на этих местах: Не могу удержаться от иллюстрации итоговой системы: Ответ: Однако предостерегаю Вас от шапкозакидательского настроения – это была несложная демонстрационная задача. Для метода Гаусса-Йордана характерны свои специфические приёмы и не самые удобные вычисления, поэтому, пожалуйста, настройтесь на серьёзную работу. Не хочу показаться резким, но во многих источниках этот метод разобран из рук вон плохо, но за годы практики мне удалось выработать оптимальный алгоритм – без мучений и зубодробительных расчётов: Пример 123 Решить систему линейных уравнений методом Гаусса-Йордана Решение: первая часть задания хорошо знакома: Очевидно, что система имеет бесконечно много решений, и наша задача – привести её расширенную матрицу к виду Как действовать дальше? Прежде всего, следует отметить, что мы лишились вкусного элементарного преобразования – перестановки строк. Точнее говоря, переставить-то их можно, но в этом нет смысла (просто выполним лишние действия). И далее целесообразно придерживаться следующего шаблона: (5) Первую строку умножаем на –3, вторую строку умножаем на 3. Вообще говоря, первую строку можно было умножить тоже на 3, но это менее удобный вариант для последующего действия. К хорошему привыкаешь быстро: В результате элементарных преобразований получена эквивалентная исходной система Заметьте, что первая базисная переменная равна константе (двойке), так бывает. Осталось записать Разумеется, крайне желательна проверка, которая выполняется по обычной схеме. А если вдруг нужно найти фундаментальную систему и записать решение в векторной форме, то это мы тоже подробнейшим образом разобрали. Для самостоятельного решения: Пример 124 Найти базисное решение с помощью элементарных преобразований Такая формулировка условия предполагает использование метода Гаусса-Йордана, и в образце решения матрица приведена к стандартному виду Так, например, если в первом столбце большие числа, то вполне допустимо привести матрицу к виду Но всё-таки это крайние случаи – не стОит лишний раз шокировать преподавателей своими знаниями, техникой решения и уж тем более не надо выдавать экзотических результатов вроде
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих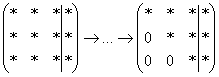 (конкретный случай для примера).
(конкретный случай для примера). 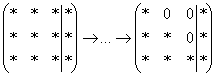 ?
? 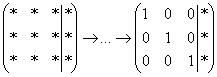 , получая готовый ответ.
, получая готовый ответ.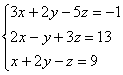
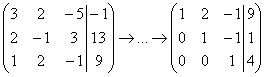
 ,
, 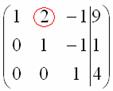 .
.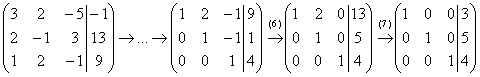
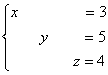
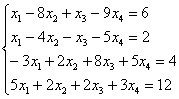
 .
.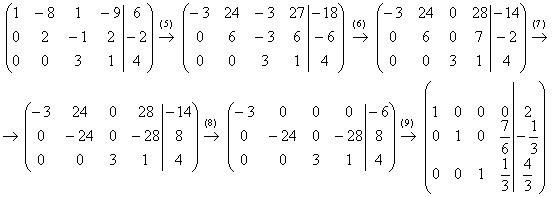
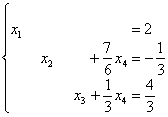
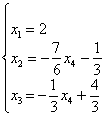
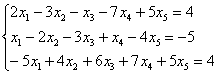
 с базисными переменными
с базисными переменными  (базисные переменные
(базисные переменные  (базисные переменные
(базисные переменные  с базисными переменными
с базисными переменными 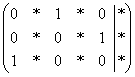 . Впрочем, бывает трудно удержаться от нетипового варианта, когда в исходной матрице, скажем, в 5-м столбце есть два готовых нуля.
. Впрочем, бывает трудно удержаться от нетипового варианта, когда в исходной матрице, скажем, в 5-м столбце есть два готовых нуля. 5.11. Как найти обратную матрицу методом элементарных преобразований?
5.11. Как найти обратную матрицу методом элементарных преобразований? 5.9.3. Взаимосвязь решений неоднородной и однородной системы
5.9.3. Взаимосвязь решений неоднородной и однородной системы