6.2. Основные понятия векторного пространства
Информация параграфа будет восприниматься намного легче, если Вы успели познакомиться с понятием линейной независимости и базисом геометрических векторов – «плоский» и пространственный случаи. И сейчас мы разберём всё это в общем виде.
Линейной комбинацией векторов 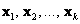 линейного пространства линейного пространства 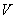 называют выражение вида называют выражение вида 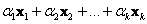 , где , где 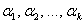 – действительные числа. – действительные числа.
Простенькие примеры из геометрии: 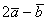 , , 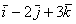 и что-нибудь поинтереснее: и что-нибудь поинтереснее: 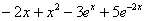 – линейная комбинация четырёх непрерывных на – линейная комбинация четырёх непрерывных на 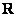 функций. функций.
Два вектора коллинеарны, если один из них можно линейно (через множитель-константу) выразить через другой: 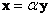 , где , где 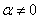 – действительное число; ну или наоборот: – действительное число; ну или наоборот: 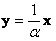 . Так, «школьные» векторы . Так, «школьные» векторы 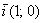 и и 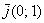 – не коллинеарны (ибо такого множителя нет), а вот векторы – не коллинеарны (ибо такого множителя нет), а вот векторы 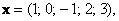 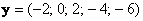 – да, поскольку – да, поскольку 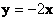 . Очевидно, что соответствующие координаты коллинеарных векторов арифметического пространства «эр эн» пропорциональны. Хотя это бывает и не очевидно :) . Очевидно, что соответствующие координаты коллинеарных векторов арифметического пространства «эр эн» пропорциональны. Хотя это бывает и не очевидно :)
И более экзотический пример: многочлены 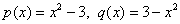 – коллинеарны, так как один линейно выражается через другой: – коллинеарны, так как один линейно выражается через другой: 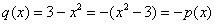 . .
Векторы 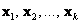 векторного пространства векторного пространства 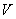 называют линейно зависимыми, если хотя бы один из них можно линейно выразить через остальные. В частности, линейно зависимы коллинеарные векторы. называют линейно зависимыми, если хотя бы один из них можно линейно выразить через остальные. В частности, линейно зависимы коллинеарные векторы.
Сформулируем определение более формально: если существует набор действительных чисел 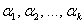 , среди которых хотя бы одно отлично от нуля, и при этом линейная комбинация , среди которых хотя бы одно отлично от нуля, и при этом линейная комбинация 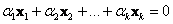 – равна нулю, то векторы – равна нулю, то векторы 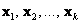 – линейно зависимы. И в самом деле, пусть, например, – линейно зависимы. И в самом деле, пусть, например, 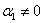 . Тогда первый вектор можно линейно выразить через остальные: . Тогда первый вектор можно линейно выразить через остальные: 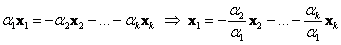 . .
Противоположно: векторы 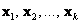 линейно независимы, если их линейная комбинация линейно независимы, если их линейная комбинация 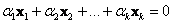 – равна нулю ТОЛЬКО В ТОМ случае, если ВСЕ множители равны нулю – равна нулю ТОЛЬКО В ТОМ случае, если ВСЕ множители равны нулю 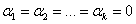 . Иными, словами, никакой из этих векторов невозможно выразить через остальные. . Иными, словами, никакой из этих векторов невозможно выразить через остальные.
Так, линейная комбинация знакомых векторов 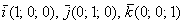 нашего пространства нашего пространства 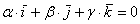 – равна нулю только в том случае, если ВСЕ коэффициенты нулевые – равна нулю только в том случае, если ВСЕ коэффициенты нулевые 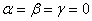 , поэтому векторы , поэтому векторы 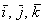 линейно независимы. линейно независимы.
Окромя геометрии, можно рассмотреть векторы любого линейного пространства, скажем, непрерывные на 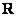 функции функции 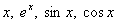 . Как многие правильно подозревали, никакую из этих функций невозможно выразить через остальные с помощью числовых множителей. Поэтому линейная комбинация . Как многие правильно подозревали, никакую из этих функций невозможно выразить через остальные с помощью числовых множителей. Поэтому линейная комбинация 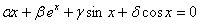 – только тогда, когда все коэффициенты равны нулю – только тогда, когда все коэффициенты равны нулю 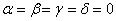 . Следовательно, эти функции линейно независимы, до скорых встреч в дифференциальных уравнениях! . Следовательно, эти функции линейно независимы, до скорых встреч в дифференциальных уравнениях!
Размерностью векторного пространства 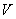 называют максимальное количество линейно независимых векторов. называют максимальное количество линейно независимых векторов.
Обозначение: 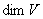 (от англ. dimension – размерность). (от англ. dimension – размерность).
Любой упорядоченный набор таких векторов образует базис данного пространства, и любой другой вектор можно разложить по базису (представить в виде линейной комбинации базисных векторов). Причём, это разложение единственно.
Размерность может быть конечна либо бесконечна.
Ярким примером конечномерного пространства является арифметическое пространство 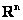 , и из школьных геометрических примеров («плоский» , и из школьных геометрических примеров («плоский» 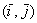 и пространственный и пространственный 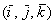 базисы) интуитивно понятно, что базисы) интуитивно понятно, что 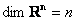 (хотя, это, конечно, строго доказывается в теории). Как вы помните, любой вектор можно единственным образом разложить по координатным векторам: (хотя, это, конечно, строго доказывается в теории). Как вы помните, любой вектор можно единственным образом разложить по координатным векторам: 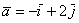 (плоскость), (плоскость), 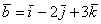 (пространство) и этот принцип легко сформулировать в общем виде: (пространство) и этот принцип легко сформулировать в общем виде:
векторы 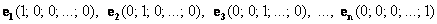 образуют базис в образуют базис в 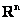 , и любой вектор сего пространства можно единственным способом разложить по этому базису: , и любой вектор сего пространства можно единственным способом разложить по этому базису: 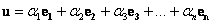 , где , где 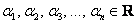 . .
Пример бесконечномерного векторного пространства, не менее яркий – это множество многочленов одной переменной с базисом из бесконечного количества линейно независимых функций 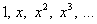 . Ежу понятно, любой многочлен можно разложить по такому базису, причём единственным образом: . Ежу понятно, любой многочлен можно разложить по такому базису, причём единственным образом: 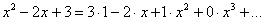
…Существует ли пространство размерности ноль? Конечно. Это тривиальный конечный случай: нульмерное векторное пространство содержит единственный вектор – нулевой. Например, 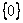 – множество, состоящее из нуля, – множество, состоящее из нуля, 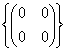 – из нулевой матрицы «два на два»; множество, состоящее из тривиального решения однородной системы и так далее. Легко убедиться, что для этих множеств выполнены все постулаты линейного пространства.Самостоятельно домучиваем матрицы «два на три»: – из нулевой матрицы «два на два»; множество, состоящее из тривиального решения однородной системы и так далее. Легко убедиться, что для этих множеств выполнены все постулаты линейного пространства.Самостоятельно домучиваем матрицы «два на три»:
Задание 2: записать базис линейного пространства 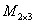 , указать размерность пространства (с обоснованием) и разложить вектор , указать размерность пространства (с обоснованием) и разложить вектор 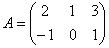 по этому базису. по этому базису.
Образец для сверки в конце книги (после решения Примера 128).
Теперь вернёмся к определению базиса, перепишу его в человеческом виде:)
Базисом 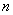 -мерного линейного пространства называют упорядоченный набор -мерного линейного пространства называют упорядоченный набор 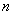 линейно независимых векторов. линейно независимых векторов.
Во-первых, обратим внимание на слово, которое я снова подчеркнул. Оно означает, что порядок базисных векторов имеет принципиальное значение, таким образом, 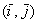 и и 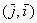 – это разные базисы (к примеру). – это разные базисы (к примеру).
Во-вторых, в определении речь идёт об 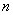 линейно независимых векторах, но ничего не сказано об их координатах. И спрашивается, а почему у векторов непременно должны быть стильные координаты с единицами? Вовсе не должны! Это могут быть и другие действительные числа – важно только, чтобы векторы были линейно независимы. Таким образом, базисов существует великое множество. линейно независимых векторах, но ничего не сказано об их координатах. И спрашивается, а почему у векторов непременно должны быть стильные координаты с единицами? Вовсе не должны! Это могут быть и другие действительные числа – важно только, чтобы векторы были линейно независимы. Таким образом, базисов существует великое множество.
Хорошо, но тут возникает другой вопрос: а как определить – вот векторы 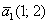 и и 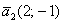 образуют базис или нет? Или векторы образуют базис или нет? Или векторы 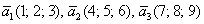 ? Такие задачи мы решали в курсе геометрии для двух- и трёхмерного случая, причём, даже не единственным способом, но сейчас я приведу лишь универсальный алгебраический критерий, обобщив его на «эн-мерный» случай: векторы ? Такие задачи мы решали в курсе геометрии для двух- и трёхмерного случая, причём, даже не единственным способом, но сейчас я приведу лишь универсальный алгебраический критерий, обобщив его на «эн-мерный» случай: векторы 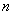 -мерного пространства -мерного пространства 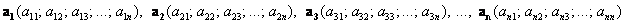 линейно независимы (а значит, образуют базис) тогда и только тогда, когда определитель, составленный из их координат, отличен от нуля: линейно независимы (а значит, образуют базис) тогда и только тогда, когда определитель, составленный из их координат, отличен от нуля:

Базис обычно обозначают перечислением его векторов в скобках: 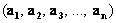
Противоположно: векторы 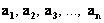 линейно зависимы и базиса НЕ образуют в том и только том случае, если определитель, составленный из их координат равен нулю. Набор таких векторов учитывает не все измерения линейно зависимы и базиса НЕ образуют в том и только том случае, если определитель, составленный из их координат равен нулю. Набор таких векторов учитывает не все измерения 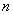 -мерного пространства, поэтому далеко не каждый вектор пространства можно выразить через этот набор. -мерного пространства, поэтому далеко не каждый вектор пространства можно выразить через этот набор.
Так, для школьных векторов 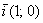 , , 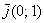 : :
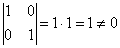 , значит, эти векторы линейно независимы и образуют базис на плоскости. Как вы прекрасно знаете, любой «плоский» вектор можно разложить по этому базису, причём, единственным образом. , значит, эти векторы линейно независимы и образуют базис на плоскости. Как вы прекрасно знаете, любой «плоский» вектор можно разложить по этому базису, причём, единственным образом.
И для векторов «университетских»:
Пример 129
Проверить, образуют ли векторы 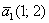 , , 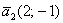 базис и найти координаты вектора базис и найти координаты вектора 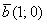 в этом базисе. в этом базисе.
Если у Вас курс алгебры, то не нужно вкладывать в такие задачи геометрический (или какой-то другой) смысл. Понимайте условие максимально абстрактно: предложенные векторы – это просто упорядоченные наборы чисел арифметического пространства 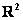 . Хотя, в условии даже и о пространстве ничего не сказано, а там могут быть свои тараканы. . Хотя, в условии даже и о пространстве ничего не сказано, а там могут быть свои тараканы.
Поэтому решение лучше оформить максимально лаконично, но тут ещё, конечно будут важные комментарии: вычислим определитель, составленный из координат векторов 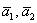 : :
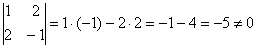 , значит, векторы линейно независимы и образуют базис. , значит, векторы линейно независимы и образуют базис.
При этом координаты векторов лучше записывать в столбцы (а не в строки). Определитель от этого не изменится, а вот технической путаницы не будет.
Так как векторы 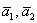 образуют базис, то любой вектор данного пространства можно единственным образом разложить по этому базису. Представим вектор «бэ» в виде линейной комбинации базисных векторов: образуют базис, то любой вектор данного пространства можно единственным образом разложить по этому базису. Представим вектор «бэ» в виде линейной комбинации базисных векторов:
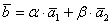 , где , где 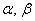 – пока ещё неизвестные нам координаты вектора – пока ещё неизвестные нам координаты вектора 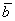 в базисе в базисе 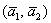 . Распишем линейную комбинацию покоординатно: . Распишем линейную комбинацию покоординатно:
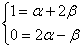 – в результате получена система двух линейных уравнений с двумя неизвестными, которую можно сразу записывать привычным образом: – в результате получена система двух линейных уравнений с двумя неизвестными, которую можно сразу записывать привычным образом:
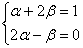
Откуда берутся коэффициенты системы? Коэффициенты слева «снимаются» из определителя (см. выше), в котором координаты базисных векторов записаны в столбцы. И свободные члены справа – это, очевидно, координаты вектора «бэ».
Систему решим по формулам Крамера. Главный определитель уже рассчитан выше 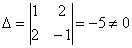 , значит, система имеет единственное решение (ну ещё бы, ведь разложение вектора по базису – единственно). , значит, система имеет единственное решение (ну ещё бы, ведь разложение вектора по базису – единственно).
Остальное – дело небольшой, даже малой техники:
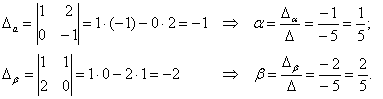
Устно проверяем, что найденные значения 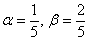 удовлетворяют каждому уравнению системы. удовлетворяют каждому уравнению системы.
В результате: 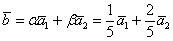 – разложение вектора – разложение вектора 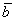 по базису по базису 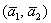 . .
Ответ: 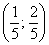 – координаты вектора – координаты вектора 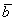 в этом базисе. в этом базисе.
И вообще, любой вектор данного пространства можно однозначно разложить по базису 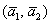 . Таким образом, новый базис меняет «координатную сетку» пространства и координаты. Вот оно как. Следующее задание для самостоятельного решения: . Таким образом, новый базис меняет «координатную сетку» пространства и координаты. Вот оно как. Следующее задание для самостоятельного решения:
Пример 130
Проверить, образуют ли следующие векторы базис, и найти координаты вектора 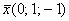 в этом базисе: в этом базисе:
а) 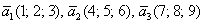 , б) , б) 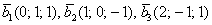 . .
В образце система решена по формулам Крамера – в подобных задачах котируется именно этот метод. Видимо потому, что часто получаются дробные координаты. …Что делать, если векторы базиса не образуют? Просто записываем этот факт в ответ – на «нет» и разложения нет :)
Очевидно, некоторые базисы менее удобны, а некоторые – более удобны для восприятия и описания 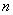 -мерного линейного пространства. Какой самый выгодный вариант? Чаще всего (но не всегда) это базис: -мерного линейного пространства. Какой самый выгодный вариант? Чаще всего (но не всегда) это базис: 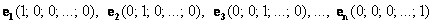 , и к нему, да и не только, мы довольно скоро вернёмся. , и к нему, да и не только, мы довольно скоро вернёмся.
 6.3. Евклидово пространство. Длина и угол 6.3. Евклидово пространство. Длина и угол
 6.1. Векторное (линейное) пространство. Так что же такое вектор? 6.1. Векторное (линейное) пространство. Так что же такое вектор?
| Оглавление |
|

 Высшая алгебра для начинающих
Высшая алгебра для начинающих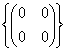 – из нулевой матрицы «два на два»; множество, состоящее из
– из нулевой матрицы «два на два»; множество, состоящее из 
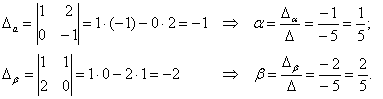
 6.3. Евклидово пространство. Длина и угол
6.3. Евклидово пространство. Длина и угол 6.1. Векторное (линейное) пространство. Так что же такое вектор?
6.1. Векторное (линейное) пространство. Так что же такое вектор?