|
Ваш репетитор, справочник и друг!
|
6.3. Евклидово пространство. Длина и уголДействительное векторное пространство
Обращаю внимание, что это определение (как и определение самого векторого пространства) имеет «максимально широкий охват». Векторы пространства Обозначения: в зависимости от темы, пространства и стиля скалярное произведение могут рисовать по-разному: Зачем нужно скалярное произведение? …О-го-го! Оно позволяет задать в линейном пространстве такие понятия, как длину вектора, и угол между ними. Длиной вектора Угол между векторами Векторы И прежде, чем перейти к конкретным примерам, ответим на вопрос существования: а можно ли в векторном пространстве вообще задать скалярное произведение? Вдруг нельзя? Теория радует нас приятным фактом на этот счёт: в любом линейном пространстве конечной размерности можно задать скалярное произведение, а значит, определить длины векторов и углы между ними. Бесконечномерный случай оставлю для самостоятельного изучения – тем, кто заинтересовался алгеброй. Теперь примеры. Рассмотрим арифметическое пространство Задание 3: доказать, что вышеуказанное правило – есть скалярное произведение. Выполняем письменно, сверяемся (после решения Примера 130), анализируем недочёты ;) и продолжаем. Коль скоро скалярное произведение задано, то длина вектора определяется по формуле Частные случаи сих формул мы встречали в геометрии, и они кажутся незыблемыми, однако это не так: эти формулы работают лишь в ортонормированных базисах. Базис называют ортонормированным, если его векторы попарно ортогональны (каждый с каждым) и имеют единичную длину. В частности, ортонормированным является декартов базис: Легко понять, что угол между любой парой векторов равен Следует заметить, что координаты векторов ортонормированного базиса не обязаны быть такими красивыми, изучИте простенький двумерный пример: Если же мы выбираем другой базис (не ортонормированный), то скалярное произведение будет задаваться иначе, а значит, и другими будут формулы длины и угла. Так, в Примере 129 я разложил вектор Разумеется, скалярное произведение можно задавать и в других векторных пространствах, даже нульмерных. Так, скалярное произведение двух непрерывных на отрезке Определённый интеграл от произведения непрерывных функций всегда существует, и он – есть вещественное число, а аксиомы скалярного произведения проверяются с помощью свойств определённого интеграла. Они выполнены (поверьте пока на слово), а значит, сия формула задаёт скалярное произведение, и пространство Да, это, конечно, необычно звучит – «угол между функциями», однако никаких проблем с нахождением таких абстрактных углов нет. Пожалуйста, для двух непрерывных и ненулевых на отрезке Само собой, понятие длины вектора здесь тоже абстрактно. На этом курс молодого линалиста закончен, дополнительную информацию можно найти, например, в следующих источниках: ИЛЬИН В. А., ПОЗНЯК Э. Г. Линейная алгебра: Учебник для вузов — 4-е изд. — М. Наука. Физматлит, 1999 и стОящий ресурс Сети, где теория изложена весьма хорошо: mathhelpplanet.com Мы же приступаем к практической эксплуатации векторных пространств:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Высшая алгебра для начинающих
Высшая алгебра для начинающих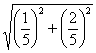 . С общей формулой скалярного произведения (и иже с ним формулами) в произвольном базисе пространства
. С общей формулой скалярного произведения (и иже с ним формулами) в произвольном базисе пространства 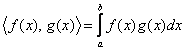 .
. 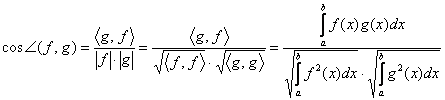
 6.4. Линейные преобразования
6.4. Линейные преобразования 6.2. Основные понятия векторного пространства
6.2. Основные понятия векторного пространства