|
Ваш репетитор, справочник и друг!
|
2.2.4. Как составить уравнение прямой по двум точкам?Уравнение прямой, которая проходит через точки На самом деле это разновидность уравнения Задача 65 Составить уравнение прямой по двум точкам Решение: используем формулу: Ответ: Проверка очевидна – координаты исходных точек должны удовлетворять полученному уравнению: 1) Подставим координаты точки 2) Подставим координаты точки Вывод: уравнение прямой составлено правильно. Если хотя бы одна из точек не удовлетворяет уравнению, ищите ошибку. Стоит отметить, что это как раз тот случай, где графическая проверка затруднительна, поскольку построить прямую Отмечу ещё пару технических моментов решения. В данной задаче несколько выгоднее воспользоваться «зеркальной» формулой Таки дробей поменьше. Если хотите, можете довести решение до конца, в результате должно получиться то же самое уравнение. Второй момент состоит в том, чтобы посмотреть на итоговый ответ и прикинуть, а нельзя ли его ещё упростить? Так, если получилось уравнение Получив ответ Задача 66 Составить уравнение прямой, проходящей через точки Это пример для самостоятельного решения, который как раз позволит лучше понять и отработать технику вычислений. Аналогично предыдущему параграфу, если в формуле
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»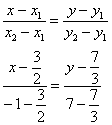
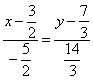
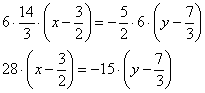
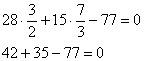
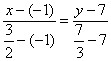
 2.2.5. Нормальный вектор прямой
2.2.5. Нормальный вектор прямой 2.2.3. Как найти направляющий вектор по общему уравнению прямой?
2.2.3. Как найти направляющий вектор по общему уравнению прямой?