3.3.2. Определение эллипса. Фокусы эллипса
Эллипс – это частный случай овала, и его строгое определение таково:
Эллипс – это множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек 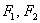 , называемых фокусами эллипса, равна длине большой оси: , называемых фокусами эллипса, равна длине большой оси: 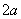 . При этом расстояния между фокусами меньше этого значения . При этом расстояния между фокусами меньше этого значения 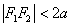 . .
Сейчас станет понятнее:
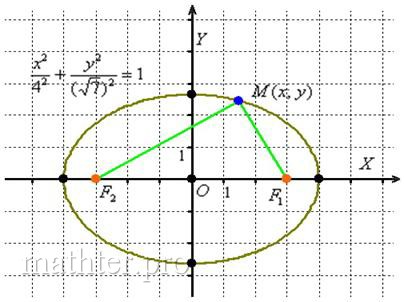
Представьте, что синяя точка «ездит» по эллипсу. Так вот,
какую бы точку эллипса 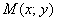 мы ни взяли, сумма длин отрезков мы ни взяли, сумма длин отрезков 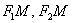 всегда будет одной и той же: всегда будет одной и той же:
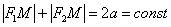
Убедимся, что в нашем примере значение суммы 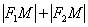 будет равно 8. Мысленно
поместите точку «эм» в правую вершину эллипса, где хорошо видно, что: будет равно 8. Мысленно
поместите точку «эм» в правую вершину эллипса, где хорошо видно, что:
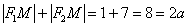
На определении эллипса основан ещё один способ его вычерчивания. Пожалуйста, возьмите ватман либо большой лист картона и приколотите его к столу
двумя гвоздиками. Это будут фокусы 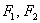 . К торчащим шляпкам гвоздей привяжите
зелёную нитку и до упора оттяните её карандашом. Гриф карандаша окажется в некоторой точке . К торчащим шляпкам гвоздей привяжите
зелёную нитку и до упора оттяните её карандашом. Гриф карандаша окажется в некоторой точке 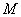 , которая принадлежит эллипсу. Теперь начинайте вести карандаш по листу бумаги, сохраняя зелёную нить сильно
натянутой. Продолжайте процесс до тех пор, пока не вернётесь в исходную точку…, отлично! – чертёж можно сдать на проверку , которая принадлежит эллипсу. Теперь начинайте вести карандаш по листу бумаги, сохраняя зелёную нить сильно
натянутой. Продолжайте процесс до тех пор, пока не вернётесь в исходную точку…, отлично! – чертёж можно сдать на проверку врачу преподавателю
=)
Как найти фокусы эллипса?
В приведённом примере я изобразил «готовенькие» точки фокуса, и сейчас мы научимся добывать их из недр фигуры.
Если эллипс задан каноническим уравнением 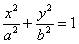 , то его фокусы имеют
координаты , то его фокусы имеют
координаты 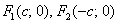 , где , где 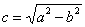 – это расстояние от каждого из фокусов до центра симметрии эллипса. – это расстояние от каждого из фокусов до центра симметрии эллипса.
Вычисления простецкие:
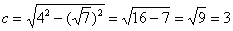 , таким образом: , таким образом: 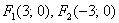
Внимание! Со значением 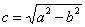 нельзя отождествлять
конкретные координаты фокусов! Повторюсь, что это РАССТОЯНИЕ от каждого из фокусов до центра (который в общем случае не обязан
располагаться именно в начале координат). Иными словами, эллипс можно перенести в другое место и значение нельзя отождествлять
конкретные координаты фокусов! Повторюсь, что это РАССТОЯНИЕ от каждого из фокусов до центра (который в общем случае не обязан
располагаться именно в начале координат). Иными словами, эллипс можно перенести в другое место и значение 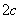 останется неизменным, в то время как фокусы, естественно, поменяют свои координаты. останется неизменным, в то время как фокусы, естественно, поменяют свои координаты.
 3.3.3. Эксцентриситет эллипса и его геометрический смысл 3.3.3. Эксцентриситет эллипса и его геометрический смысл
 3.3.1 Каноническое уравнение и построение эллипса 3.3.1 Каноническое уравнение и построение эллипса
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»
 3.3.3. Эксцентриситет эллипса и его геометрический смысл
3.3.3. Эксцентриситет эллипса и его геометрический смысл 3.3.1 Каноническое уравнение и построение эллипса
3.3.1 Каноническое уравнение и построение эллипса