3.3.1. Каноническое уравнение эллипса.
Как построить эллипс?
Во-первых, правописание…. Пожалуйста, не повторяйте ошибок некоторых юзеров, которые запрашивают «элипс», «эллибз» и даже «элебс» :) Эллипс.
Каноническое уравнение эллипса имеет вид 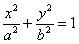 , где , где 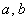 – положительные действительные числа, причём – положительные действительные числа, причём 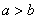 . Определение эллипса я сформулирую чуть позже, а пока самое время отдохнуть от говорильни и решить распространённую
задачу: . Определение эллипса я сформулирую чуть позже, а пока самое время отдохнуть от говорильни и решить распространённую
задачу:
Как построить эллипс?
Да, вот взять его и просто начертить. Задание встречается часто, и значительная часть студентов не совсем грамотно справляются с
чертежом:
Задача 96
Построить эллипс, заданный уравнением 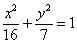
Решение: сначала приведём уравнение к каноническому виду:
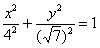
Зачем приводить? Большое преимущество канонического уравнения 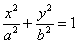 заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках заключается в том, что оно позволяет моментально определить вершины эллипса, которые находятся в точках 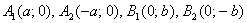 . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению . Легко заметить, что координаты каждой из этих точек удовлетворяют уравнению 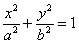 . .
В нашем случае 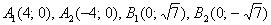 : :
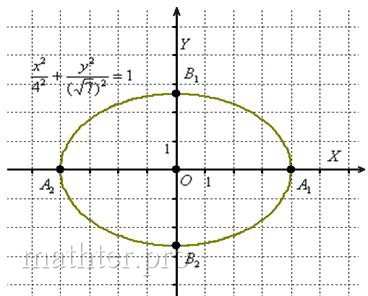 Число Число 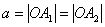 называют большой полуосью эллипса; называют большой полуосью эллипса;
число 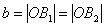 – малой полуосью; – малой полуосью;
отрезок 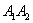 называют большой осью эллипса; называют большой осью эллипса;
отрезок 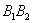 – малой осью. – малой осью.
Очевидно, что значения «а» и «бэ» (в нашем примере 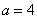 , , 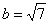 ) вместе центром симметрии (в нашем примере ) вместе центром симметрии (в нашем примере 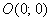 ) однозначно определяют эллипс. ) однозначно определяют эллипс.
Всё выглядит красиво, ладно, но есть один нюанс: я выполнил чертёж с помощью Приложения Геометрический Калькулятор. И вы
тоже можете так поступить. Однако в суровой действительности на столе лежит клетчатый листок бумаги, и на наших руках водят хоровод мыши. Люди с художественным талантом,
конечно, могут поспорить, но мыши есть и у вас (правда, поменьше). Поэтому для ручного построения чертежа крайне желательно найти дополнительные
точки.
Существует два подхода к построению эллипса – геометрический и алгебраический. Построение с помощью циркуля и линейки мне не нравится по причине
замороченного алгоритма и существенной загроможденности чертежа. В случае крайней необходимости обратитесь к учебнику, а в реальности же гораздо
удобнее воспользоваться средствами алгебры. Из уравнения эллипса 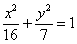 на
черновике быстренько выражаем: на
черновике быстренько выражаем:
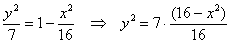
Далее уравнение распадается на две функции:
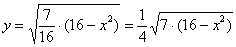 – определяет верхнюю дугу эллипса; – определяет верхнюю дугу эллипса;
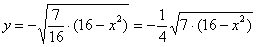 – определяет нижнюю дугу эллипса. – определяет нижнюю дугу эллипса.
Каноничный эллипс симметричен относительно координатных осей, а также относительно начала координат. И это отлично! – ибо работы
будет в 4 раза меньше. Рассмотрим 1-ю координатную четверть, соответствующую функцию 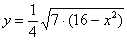 , и здесь напрашивается найти точки с абсциссами , и здесь напрашивается найти точки с абсциссами 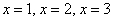 : :
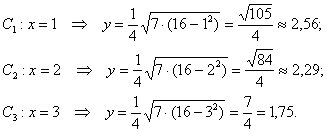
 Безусловно, приятно и то, что если допущена серьёзная ошибка
в вычислениях, то это сразу же выяснится в ходе построения. Безусловно, приятно и то, что если допущена серьёзная ошибка
в вычислениях, то это сразу же выяснится в ходе построения.
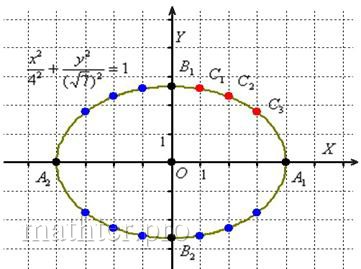
Отметим на чертеже точки 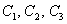 (красный цвет), симметричные точки на остальных
дугах (синий цвет) и аккуратно соединим линией всю компанию: (красный цвет), симметричные точки на остальных
дугах (синий цвет) и аккуратно соединим линией всю компанию:
Первоначальный набросок лучше прочертить тонко-тонко, и только потом придать нажим карандашу.
В результате должен получиться вполне симпатичный эллипс.
Кстати, не желаете ли узнать, что это за кривая?
 3.3.2. Определение эллипса. Фокусы эллипса 3.3.2. Определение эллипса. Фокусы эллипса
 3.2. Классификация линий второго порядка 3.2. Классификация линий второго порядка
| Оглавление |
|