3.2. Классификация линий второго порядка
Вернёмся к общему уравнению 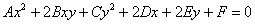 и вспомним его простейшие школьные вариации.
В качестве примера напрашивается парабола и вспомним его простейшие школьные вариации.
В качестве примера напрашивается парабола 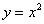 , уравнение которой легко привести к
общему виду: , уравнение которой легко привести к
общему виду: 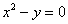 . Однако не всё так
гладко…. . Однако не всё так
гладко….
Существенный недостаток общего уравнения состоит в том, что почти всегда не понятно, какую линию оно задаёт. Даже в простейшем
случае 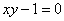 не сразу сообразишь, что это гипербола. Поэтому в курсе
аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду – виду, в
котором сразу понятно, что это за линия и как она выглядит. не сразу сообразишь, что это гипербола. Поэтому в курсе
аналитической геометрии рассматривается типовая задача приведения уравнения линии 2-го порядка к каноническому виду – виду, в
котором сразу понятно, что это за линия и как она выглядит.
И если любая линия 1-го порядка представляет собой прямую, то на втором этаже нас уже ждёт более разнообразная компания. С помощью
специального комплекса действий (который мы освоим позже) общее уравнение линии второго порядка 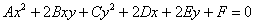 приводится к одному из следующих видов ( приводится к одному из следующих видов (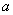 и и 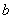 – положительные действительные
числа): – положительные действительные
числа):
1) 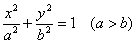 – каноническое уравнение эллипса; – каноническое уравнение эллипса;
2) 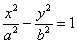 – каноническое уравнение гиперболы; – каноническое уравнение гиперболы;
3) 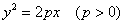 – каноническое уравнение параболы; – каноническое уравнение параболы;
4) 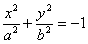 – мнимый эллипс; – мнимый эллипс;
5) 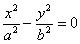 – пара пересекающихся прямых; – пара пересекающихся прямых;
6) 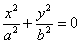 – пара мнимых пересекающихся прямых с единственной действительной точкой
пересечения в начале координат; – пара мнимых пересекающихся прямых с единственной действительной точкой
пересечения в начале координат;
7) 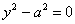 – пара параллельных прямых; – пара параллельных прямых;
8) 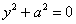 – пара мнимых параллельных прямых; – пара мнимых параллельных прямых;
9) 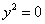 – пара совпавших прямых. – пара совпавших прямых.
Возможно, у вас сложилось впечатление неполноты списка. Например, в пункте 7 уравнение 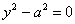 задаёт пару прямых задаёт пару прямых 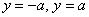 , параллельных оси , параллельных оси 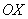 , и возникает вопрос: а где
же уравнение , и возникает вопрос: а где
же уравнение 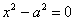 , определяющее прямые , определяющее прямые 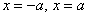 , параллельные оси ординат? Ответ: оно хоть и эквивалентно, но не считается каноническим. Прямые , параллельные оси ординат? Ответ: оно хоть и эквивалентно, но не считается каноническим. Прямые 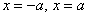 представляют собой тот же самый случай представляют собой тот же самый случай 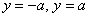 , повёрнутый на 90 градусов, и дополнительная запись , повёрнутый на 90 градусов, и дополнительная запись 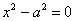 в классификации избыточна, поскольку не несёт ничего принципиально нового. в классификации избыточна, поскольку не несёт ничего принципиально нового.
Таким образом, существует девять и только девять различных видов линий второго порядка, но особый интерес представляют эллипс,
гипербола и парабола. Рассмотрим их по порядку:
 3.3. Эллипс 3.3. Эллипс
 3.1. Алгебраическая линия и её порядок 3.1. Алгебраическая линия и её порядок
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» 3.3. Эллипс
3.3. Эллипс 3.1. Алгебраическая линия и её порядок
3.1. Алгебраическая линия и её порядок