|
Ваш репетитор, справочник и друг!
|
3.8. Приведение уравнения к каноническому видуЭта задача следовала за нами практически с самого начала главы и в заключительном параграфе мы окончательно разберёмся, как общее уравнение линии второго порядка В предыдущих параграфах мы очень подробно отработали частный случай уравнения, когда коэффициент Такое уравнение приводится методом выделения полного квадрата(ов) с дальнейшим применением формул …У вас такое уравнение? Значит, вам хватит материалов предыдущих параграфов! Не такое? Значит, не хватит :) Как многие подметили, члены Уравнение Рассмотрим в качестве примера уравнение Немного потраченного времени, и вы научитесь довольно легко находить ответы на эти вопросы, в частности, без особых проблем сможете определить,
что данное уравнение определяет эллипс с полуосями Именно поэтому и появилась задача приведения уравнения к каноническому виду – чтобы независимо от расположения линии выяснить, что это за зверь и каким нравом он обладает. 1) Осуществим параллельный перенос эллипса центром в начало координат (представляем мысленно) и повернём его на угол 2) Перейдём к прямоугольной системе координат Но стОит ли перемещать САМУ линию? Представьте, что крыша вашего дома имеет эллиптическую форму, и шаловливый Карлсон выбрал начало координат на
трубе кочегарки J. Что вы будете делать, чтобы с комфортом исследовать эллипс? Разумеется, не станете переносить крышу, а перейдёте к удобной
системе координат. То есть, система координат относительна и вторична по отношению к тому или иному объекту. Следовательно, вполне логично и правомерно тревожить именно её, а не «уникальный» эллипс, крышу дома или что-то ещё. А суть преамбулы состоит в том, что далее мы будем приводить уравнение линии 2-го порядка путём перехода к новой прямоугольной системе координат, в которой уравнение исследуемой линии примет канонический вид. Существует несколько практических методов приведения уравнения линии к каноническому виду, причём, некоторые из них являются достаточно трудными. Я постараюсь составить максимально простой конспект, доступный человеку с любым уровнем подготовки. Для этого нам потребуется ещё одно теоретическое понятие: Все линии 2-го порядка можно разделить на две большие группы: 1) центральные линии, обладающие единственным центром (точкой) симметрии (эллипс, мнимый эллипс, гипербола, пара мнимых или действительных пересекающихся прямых); 2) нецентральные линии, у которых центры симметрии отсутствуют (парабола), либо их бесконечно много (пара действительных или мнимых параллельных прямых, пара совпавших прямых). Итак, вы счастливый обладатель уравнения С чего начать? На первом шаге целесообразно выяснить, к какой группе относится линия. Для этого нужно мысленно либо на
черновике составить и вычислить определитель Для уравнения Зачем это нужно? Чтобы выбрать наиболее выгодный способ решения. Да, конечно, ваш учебный план может и не предоставить возможность выбора, но, тем не менее, я постараюсь провести вас через дебри самой комфортной и короткой тропинкой. Для приведения уравнения центральной линии, по моему мнению, лучше всего использовать метод инвариантов. Но, к сожалению, он перестаёт работать в нецентральном случае, поэтому на помощь придётся привлечь достаточно трудоёмкий универсальный способ решения либо ортогональное преобразование квадратичной формы (но тут уже надо ориентироваться в другой теме). Сначала разберём одно, затем другое, и даже если вам нужно разделаться лишь с нецентральной линией, постарайтесь не пропускать нижеследующий параграф, поскольку вся информация взаимосвязана:
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»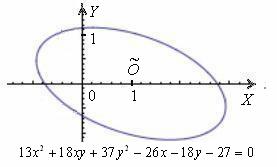 Мысленно возьмите эллипс в руки, поверните его на любой угол
и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если
вам предъявить его без чертежа, то никто в жизнь не догадается, что оно определяет тот же самый эллипс.
Мысленно возьмите эллипс в руки, поверните его на любой угол
и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если
вам предъявить его без чертежа, то никто в жизнь не догадается, что оно определяет тот же самый эллипс. 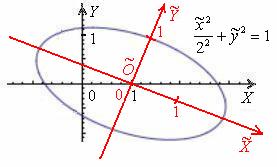 «Навскидку» второй способ кажется вычурным и неуклюжим,
однако, если немного призадуматься, то он более корректен. И толстый намёк на это уже проскочил чуть выше: куда бы мы ни переместили данную линию,
какую бы систему координат ни выбрали – эллипс останется тем же самым эллипсом с полуосями
«Навскидку» второй способ кажется вычурным и неуклюжим,
однако, если немного призадуматься, то он более корректен. И толстый намёк на это уже проскочил чуть выше: куда бы мы ни переместили данную линию,
какую бы систему координат ни выбрали – эллипс останется тем же самым эллипсом с полуосями  3.8.1. Приведение уравнения центральной линии. Метод инвариантов
3.8.1. Приведение уравнения центральной линии. Метод инвариантов 3.7.2. Директрисы гиперболы
3.7.2. Директрисы гиперболы