3.8.1. Приведение уравнения центральной линии.
Метод инвариантов
Во-первых, термин. Инвариант – это величина, которая остаётся неизменной при тех или иных преобразованиях.
Простейший пример геометрического инварианта – это длина отрезка относительно его параллельного
переноса. В результате данного преобразовании меняются координаты концов отрезка, но его длина остаётся неизменной (инвариантной).
В частности, длина, ширина и толщина учебника Фихтенгольца (который можно положить на стол, на стул, на
кровать, под кровать, в мусорное ведро) – это инварианты относительно перемещения книги в пространстве. А вот если ненавистный томик порвать в
клочья, то его размеры уже перестанут быть инвариантами относительно этих механических повреждений. Но инвариантом останется сам математический
анализ. Так что рви, не рви, а осваивать его придётся :)
Однако вернёмся к нашему демонстрационному уравнению:
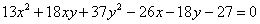
Очевидно, что можно выбрать бесконечно много других прямоугольных систем координат и получить бесконечно много различных уравнений вида 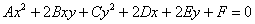 , которые задают один и тот же эллипс. , которые задают один и тот же эллипс.
И возникает вопрос: а есть ли у этого множества уравнений что-то одинаковое, характерное только для данной линии? Иными
словами, есть ли инварианты?
Да, есть!
Если линия второго порядка задана 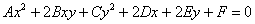 – общим уравнением в некоторой
прямоугольной системе координат, то инвариантами относительно поворота и параллельного переноса прямоугольной системы координат являются следующие ЧИСЛА: – общим уравнением в некоторой
прямоугольной системе координат, то инвариантами относительно поворота и параллельного переноса прямоугольной системы координат являются следующие ЧИСЛА:
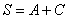 – сумма коэффициентов при – сумма коэффициентов при 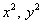 , ,
старый знакомец 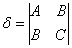
и ещё один определитель: 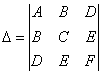 . .
Рассмотрим исходное уравнение 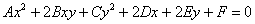 и поставим задачу
подобрать новую прямоугольную систему координат и поставим задачу
подобрать новую прямоугольную систему координат 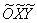 ТАК, чтобы
уравнение данной линии приняло в ней вид ТАК, чтобы
уравнение данной линии приняло в ней вид 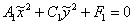 (который элементарно сводится к
канонической форме). Заметим попутно логичную вещь – коэффициенты итогового уравнения, «отвечающие» за поворот и параллельный перенос равны нулю: (который элементарно сводится к
канонической форме). Заметим попутно логичную вещь – коэффициенты итогового уравнения, «отвечающие» за поворот и параллельный перенос равны нулю: 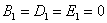
Поскольку инварианты (числа) 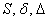 НЕ ЗАВИСЯТ от коэффициентов
того или иного уравнения, то справедливыми являются следующие равенства: НЕ ЗАВИСЯТ от коэффициентов
того или иного уравнения, то справедливыми являются следующие равенства:
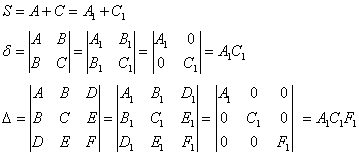
откуда следует простой и изящный алгоритм решения нашей задачи:
1) Из исходного уравнения находим числа 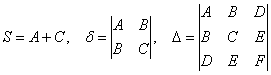 . .
2) Решаем систему 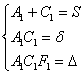 и записываем уравнение и записываем уравнение 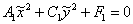 , которое легко приводится к каноническому виду. При этом угол поворота новой системы
координат , которое легко приводится к каноническому виду. При этом угол поворота новой системы
координат 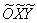 относительно старой системы относительно старой системы 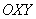 находится из уравнения находится из уравнения 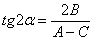 . Если . Если 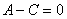 , то угол равен либо , то угол равен либо 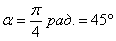 , либо , либо 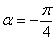 и это недостаток формулы. Но это не
беда. Потому что есть другая формула: и это недостаток формулы. Но это не
беда. Потому что есть другая формула: 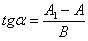 . Координаты нового начала координат . Координаты нового начала координат 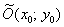 отыскиваются как решение системы отыскиваются как решение системы 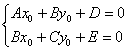 . .
Таким образом, решение нашей задачи укладывается в стройную и понятную схему, доступную даже школьнику. Выясним же, наконец, как из потрёпанного
уравнения 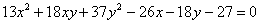 получается канонический эллипс получается канонический эллипс 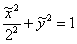 : :
Задача 111
Привести уравнение линии второго порядка к каноническому виду
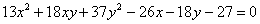
Найти начало соответствующей системы координат и угол её поворота
Решение: перейдём к новой прямоугольной системе координат 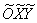 , в которой уравнение данной линии примет вид , в которой уравнение данной линии примет вид 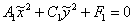 . .
На первом шаге из исходного уравнения находим коэффициенты 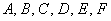 . В тетради это удобно сделать следующим образом: . В тетради это удобно сделать следующим образом:
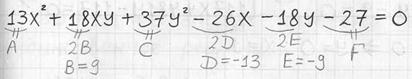
Здесь важно не потерять «минусы», а также не забыть разделить пополам нужные числа. Кроме того, некоторые слагаемые могут отсутствовать, и тогда соответствующие коэффициенты будут равны нулю – не спешим и не путаемся! В нашем
случае всё на месте и, соответственно, все коэффициенты ненулевые:
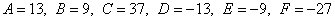
Вычислим инварианты:
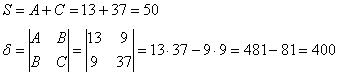
Последний определитель выгодно раскрыть с помощью элементарного преобразования, прибавив к
третьей строке первую строку:
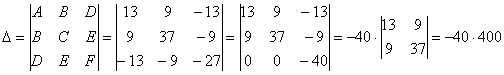
Инварианты найдены, составим и решим систему:
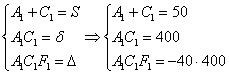
Из последних двух уравнений сразу просматривается значение коэффициента 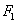 : :
поскольку 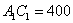 , то, подставляя это произведение в 3-е уравнение, получаем: , то, подставляя это произведение в 3-е уравнение, получаем:
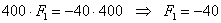
Но тут важнее разобраться с другими коэффициентами. Есть длинный путь, и есть короткий.
Путь длинный: из 1-го уравнения
выражаем 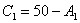 – подставляем во второе уравнение: – подставляем во второе уравнение:
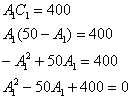
Решим квадратное уравнение:
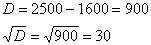
В результате получается два комплекта симметричных корней:
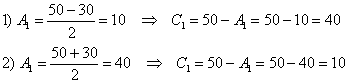
Путь короткий, к которому я рекомендую «пристреляться», в том числе, и «чайникам». Это подбор корней. Смотрим на первые два
уравнения системы: 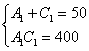 . Прикидку можно делать либо по первому уравнению, либо по
второму, кому как удобнее. Лично я привык ориентироваться по сумме коэффициентов. Правдоподобных вариантов здесь не так и много: . Прикидку можно делать либо по первому уравнению, либо по
второму, кому как удобнее. Лично я привык ориентироваться по сумме коэффициентов. Правдоподобных вариантов здесь не так и много:
0 и 50
10 и 40 – удовлетворяет и первому и второму уравнению
20 и 30
30 и 20
40 и 10 – симметричная пара корней
50 и 0
Как видите, на подходящую пару чисел мы «натыкаемся» практически сразу. В силу симметричности уравнений решением будут являться и «зеркальные»
значения 40 и 10.
Таким образом, в нашем распоряжении оказывается два набора корней:
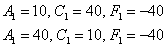
Не забываем выполнить проверку, подставив значения первого (можно второго) комплекта в левую часть каждого уравнения системы:
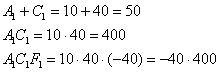
В результате получены соответствующие правые части исходных уравнений, что и требовалось проверить.
Теперь мысленно либо на черновике следует выяснить, какое решение приведёт нас к желаемому результату.
Подставляем первый комплект корней 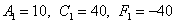 в уравнение в уравнение 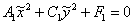 : :
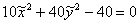
Техника завершающих преобразований хорошо знакома:
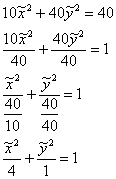
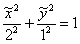 – эллипс с центром в точке – эллипс с центром в точке 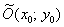 , большой полуосью , большой полуосью 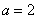 , малой полуосью , малой полуосью 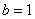 . .
Такой фразы будет достаточно – нас никто не спрашивал про фокусы, эксцентриситет и другие характеристики линии.
Всё вышло удачно с первой попытки. Если в уравнение 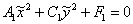 подставить второй
набор корней подставить второй
набор корней 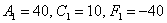 , то получится неканоническая запись того же эллипса , то получится неканоническая запись того же эллипса 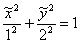 – повёрнутого на 90 градусов. – повёрнутого на 90 градусов.
Найдём угол поворота новой системы координат 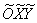 относительно старой: относительно старой:
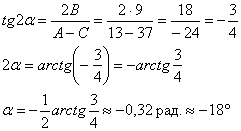
Или по второй, более лёгкой, но почему-то менее распространённой формуле:
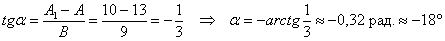
Координаты 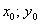 начала новой системы координат начала новой системы координат 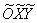 найдём как решение системы: найдём как решение системы: 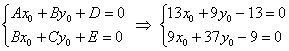
Первое уравнение умножим на 9, второе уравнение умножим на 13 и из 2-го уравнения почленно вычтем 1-е (проще способа не видно):
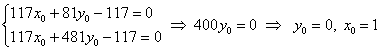 , таким образом: , таким образом: 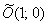 . .
В том случае если по условию необходимо выполнить чертёж – выполняем чертёж, приведённый выше. Впрочем, мне нетрудно скопировать:
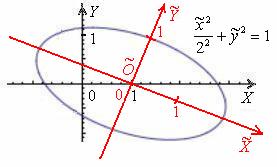 Ввиду сложности чертежа вполне допустимо его схематичное
оформление, однако всё-таки постарайтесь, чтобы рисунок был похож на правду. Как вариант, можно изобразить только новую систему координат Ввиду сложности чертежа вполне допустимо его схематичное
оформление, однако всё-таки постарайтесь, чтобы рисунок был похож на правду. Как вариант, можно изобразить только новую систему координат  и эллипс в горизонтальном положении, но тогда прокомментируйте, что она
получена поворотом системы и эллипс в горизонтальном положении, но тогда прокомментируйте, что она
получена поворотом системы  на угол на угол 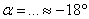 и её параллельным переносом в точку и её параллельным переносом в точку 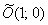 . .
Ответ: 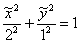 – эллипс с полуосями – эллипс с полуосями 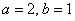 – в системе координат – в системе координат 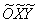 с
началом в точке с
началом в точке 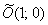 , повёрнутой относительно исходной системы координат , повёрнутой относительно исходной системы координат 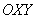 на угол на угол 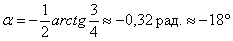 . .
Это мы рассмотрели так называемый эллиптический случай, когда коэффициенты 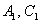 – отличны от нуля и одного знака (оба положительны либо оба отрицательны), т.е. когда их произведение – отличны от нуля и одного знака (оба положительны либо оба отрицательны), т.е. когда их произведение 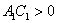 . .
И в этом случае может получиться не только эллипс. Если все три коэффициента 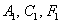 одного знака, то это мнимый эллипс. Так, если бы в рассмотренной задаче
мы получили уравнение одного знака, то это мнимый эллипс. Так, если бы в рассмотренной задаче
мы получили уравнение 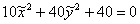 , то пришли бы к уравнению , то пришли бы к уравнению 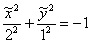 . Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа,
поскольку мнимый эллипс остаётся разве что мнить =) . Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа,
поскольку мнимый эллипс остаётся разве что мнить =)
Ещё одна разновидность эллиптического случая – нулевой свободный член: 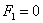 , предвестником которого является нулевой третий инвариант: , предвестником которого является нулевой третий инвариант: 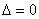 . В частности, уравнение . В частности, уравнение 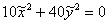 сводится к виду сводится к виду 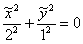 – и это пара мнимых пересекающихся
прямых с единственной действительной точкой их пересечения – и это пара мнимых пересекающихся
прямых с единственной действительной точкой их пересечения 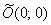 (с нулевыми
координатами в новой системе координат (с нулевыми
координатами в новой системе координат 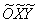 ). ).
Предлагаю самостоятельно ознакомиться с гиперболическим случаем:
Задача 112
Привести уравнение линии второго порядка к каноническому виду
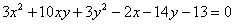 , найти начало соответствующей системы координат, угол её поворота и
выполнить чертёж. , найти начало соответствующей системы координат, угол её поворота и
выполнить чертёж.
После краткого образца решения есть важные дополнительные комментарии!
Теперь переходим к рассмотрению параболического случая 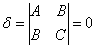 , где по очевидной
причине метод инвариантов становится непригодным: , где по очевидной
причине метод инвариантов становится непригодным:
 3.8.2. Приведение уравнения нецентральной линии 3.8.2. Приведение уравнения нецентральной линии
 3.8. Приведение уравнения к каноническому виду 3.8. Приведение уравнения к каноническому виду
| Оглавление |
|