|
Ваш репетитор, справочник и друг!
|
3.8.2. Приведение уравнения нецентральной линииИ сейчас мы, по сути, разберём частный случай универсального метода решения, который вкратце состоит в следующем: На первом шаге выясняется угол поворота системы На втором шаге выделяются полные квадраты (при необходимости) и проводится параллельный перенос системы Должен отметить неудачные обозначения со штрихами, но так принято практически во всех учебниках, и поэтому я не буду отклоняться от стандарта.
Штрихи, как вы поняли, к производным никакого отношения не имеют. В
предыдущем параграфе, к слову, я намеренно использовал обозначения Таким образом, универсальный способ приведения к линии 2-го порядка к каноническому виду предполагает два последовательных преобразования
прямоугольной системы координат – поворот и параллельный перенос: Как, наверное, вы уже догадались и горестно вздохнули, удобный метод инвариантов позволял получить то же самое «одним махом»: Но в параболическом случае мы вынуждены выехать с тихой просёлочной дороги метода инвариантов на оживлённую автостраду общего способа решения: Задача 113 Привести уравнение линии второго порядка к каноническому виду Выполнить чертёж. Решение: в первую очередь выясним тип линии. Вычислим определитель, составленный из коэффициентов 1) Осуществим поворот исходной системы координат Внимание! Данная формула справедлива только для параболического случая! В нашем примере: Очевидно, что Продолжаем: Если осуществляется поворот прямоугольной системы координат И сложившейся ситуации вполне прагматичным решением будет привлечь на помощь метод научного практического тыка. Не теряя времени, начинаем
работать с углом Итак, для угла Подставим найденные значения Подставляем Теперь нужно возвести в квадраты, раскрыть все скобки,… но что-то
не хочется. Для нецентральной линии существует эксклюзивная «фишка»: в результате рассматриваемой подстановки сумма Внимательно раскрываем скобки и приводим подобные слагаемые. И НЕ ТЕРЯЕМ ШТРИХИ: И по всем признакам получается как раз парабола. Сократим каждое слагаемое на 2 и перебросим некоторые из них в
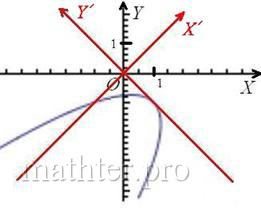
правую часть: Перед слагаемым, содержащим «икс штрих», нарисовался знак минус, и это плохо. Для лучшего понимания проиллюстрирую выполненное действие готовым
чертежом: С углом не повезло…, что делать? Если вы уже оформили решение на чистовик (что очень вероятно), то поступаем хитро. Невозмутимо выделяем в полученном уравнении полный
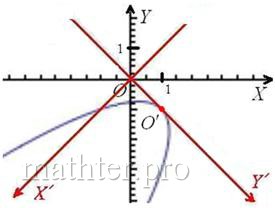
квадрат и представляем его в виде Теперь осуществляем поворот системы Проведём физкульт-разминку и заодно спасём от онемения некоторые части тела :) Пожалуйста, встаньте лицом к монитору и наклонитесь вправо на 90 градусов. Теперь поверните голову ещё на 45 градусов в том же направлении и полюбуйтесь почти канонической параболой. Если же решение ещё не оформлено на чистовик, то можно сразу выбрать угол 2) Шаг второй, параллельный перенос системы Аналитически это действие
выражается заменами Вновь наклонитесь вправо на Ответ: данная линия представляет собой параболу Интересно отметить, что для параболы метод инвариантов, хоть и не работает, но тоже позволяет
найти её каноническое уравнение. Во-первых, полезно иметь в виду следующий характеристический признак: уравнение линии 2-го
порядка, инварианты которого удовлетворяют условиям Представьте, что вы видите уравнение И, во-вторых, найденные инварианты позволяют найти фокальный параметр Таким образом: Желающие могут использовать данный путь для самопроверки или даже в качестве основного решения в критической ситуации – когда не получается найти уравнение параболы стандартным способом, но жизненно важно «родить» хоть что-то. Следующий пример для самостоятельной разработки: Задача 114 Привести уравнение линии второго порядка к каноническому виду Примерный образец чистового оформления задачи в конце книги. Следует отметить, что на практике достаточно популярна урезанная версия задачи. Случай, когда нужно выполнять только параллельный перенос,
досконально изучен в предыдущих параграфах, но бывает и так, что необходимо осуществить только поворот системы координат. Так, например, в уравнении Также полезно знать, что вырожденное уравнение параболического типа несложно выразить в явном виде и в исходной системе
координат, поскольку проходят тривиальные алгебраические преобразования. Так, для того же уравнения Полученный результат удобно использовать для проверки и выполнения чертежа. Что касается инвариантов, то дела тут обстоят хуже. Если для параболы мы ещё смогли «вытянуть»
некоторую информацию из инвариантов, то здесь будем созерцать малополезный набор Итак, систематизируем порядок действий в параболическом случае: 1) Из формулы 2) Для данного угла «альфа» рассчитываем 3) Подставляем найденные значения 4) Подставляем найденные выражения 4*) Примерно в 15% случаев может получиться уравнение, которое определяет параболу, развёрнутую относительно своего
канонического положения (положительного направления оси 5) В полученном уравнении 6) Чертёж. Если совсем тяжко, пойдёт схематический, но проявите аккуратность.
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»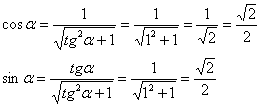
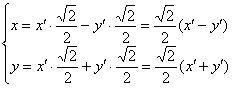
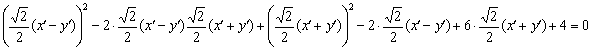
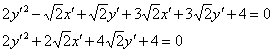
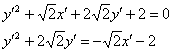
 В результате поворота исходной системы координат
В результате поворота исходной системы координат 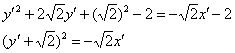
 При таком «довороте» меняется знак у «иксовой» части
уравнения, а также знаки внутри скобок:
При таком «довороте» меняется знак у «иксовой» части
уравнения, а также знаки внутри скобок: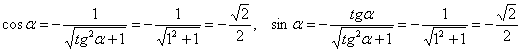 , после чего «проворачиваем» тот же алгоритм и
получаем уравнение
, после чего «проворачиваем» тот же алгоритм и
получаем уравнение 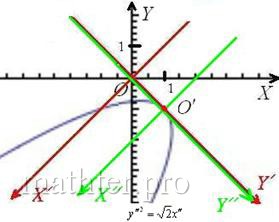 Осуществим параллельный перенос системы
Осуществим параллельный перенос системы 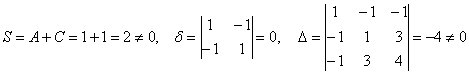
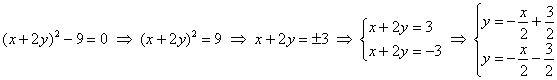
 3.8.3. Универсальный метод приведения
3.8.3. Универсальный метод приведения 3.8.1. Приведение уравнения центральной линии. Метод инвариантов
3.8.1. Приведение уравнения центральной линии. Метод инвариантов