3.5.1. Парабола – построение, каноническое уравнение,
определение, фокусы, директриса, эксцентриситет
Свершилось! Она самая. Готовая раскрыть немало тайн. Каноническое уравнение параболы имеет вид 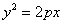 , где , где 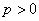 – действительное число. Нетрудно понять,
что в своём стандартном положении парабола «лежит на боку» и её вершина находится в начале координат. При этом функция – действительное число. Нетрудно понять,
что в своём стандартном положении парабола «лежит на боку» и её вершина находится в начале координат. При этом функция 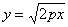 задаёт верхнюю ветвь данной линии, а функция задаёт верхнюю ветвь данной линии, а функция 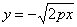 –
нижнюю ветвь. Очевидно, что парабола симметрична относительно оси –
нижнюю ветвь. Очевидно, что парабола симметрична относительно оси 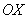 . Собственно, чего
париться, разберём всё в одной задаче: . Собственно, чего
париться, разберём всё в одной задаче:
Задача 101
Построить параболу 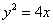
Решение: вершина параболы очевидна, найдём дополнительные точки. Уравнение 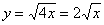 определяет верхнюю дугу параболы, уравнение определяет верхнюю дугу параболы, уравнение 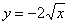 –
нижнюю дугу. Вычисления удобно провести «под одной гребёнкой» –
нижнюю дугу. Вычисления удобно провести «под одной гребёнкой» 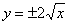 : :

Отмечаем найденные точки на чертеже и аккуратно соединяем их линией:
 Параболой называется множество всех точек плоскости,
равноудалённых от данной точки Параболой называется множество всех точек плоскости,
равноудалённых от данной точки 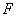 и данной прямой и данной прямой 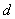 , не проходящей через точку , не проходящей через точку 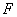 . .
Определение параболы понимается ещё проще, чем определения эллипса и гиперболы. Для любой точки 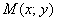 параболы
длина отрезка параболы
длина отрезка 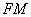 (расстояние от точки до фокуса) равна длине перпендикуляра (расстояние от точки до фокуса) равна длине перпендикуляра 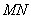 (расстоянию от точки до директрисы): (расстоянию от точки до директрисы):
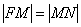
Точка 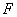 называется фокусом параболы, а прямая называется фокусом параболы, а прямая 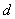 – директрисой параболы (пишется с одной «эс»). – директрисой параболы (пишется с одной «эс»).
Константа «пэ» канонического уравнения 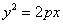 называется фокальным параметром параболы, в данном случае называется фокальным параметром параболы, в данном случае 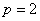 . При этом фокус имеет координаты . При этом фокус имеет координаты 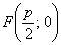 , а директриса задаётся уравнением , а директриса задаётся уравнением 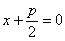 . .
В нашем примере: 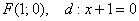 . .
Поздравляю! Многие из вас сегодня сделали самое настоящие открытие!
Оказывается, гипербола и парабола вовсе не являются графиками «рядовых» функций, а имеют ярко выраженное геометрическое происхождение.
Очевидно, что при увеличении фокального параметра ветви графика 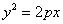 будут
«раздаваться» вверх и вниз, бесконечно близко приближаясь к оси будут
«раздаваться» вверх и вниз, бесконечно близко приближаясь к оси 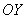 . При
уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси . При
уменьшении же значения «пэ» они начнут сжиматься и вытягиваться вдоль оси 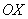
Эксцентриситет любой параболы равен единице: 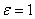
 3.5.2. Поворот и параллельный перенос параболы 3.5.2. Поворот и параллельный перенос параболы
 3.4.5. Поворот и параллельный перенос гиперболы 3.4.5. Поворот и параллельный перенос гиперболы
| Оглавление |
|