3.4.2. Определение гиперболы
У гиперболы, точно так же, как и у эллипса, есть две особенные точки 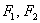 , которые называются фокусами. , которые называются фокусами.
Не говорил, но на всякий случай, вдруг кто неверно понимает: центр симметрии и точки фокуса, разумеется, не принадлежат кривым.
Общая концепция определения тоже похожа:
Гиперболой называют множество всех точек плоскости, абсолютное значение разности расстояний до каждой из которых от двух данных точек 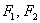 – есть
величина постоянная, равная расстоянию между вершинами данной гиперболы: – есть
величина постоянная, равная расстоянию между вершинами данной гиперболы: 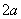 . При
этом расстояние между фокусами превосходит длину действительной оси: . При
этом расстояние между фокусами превосходит длину действительной оси: 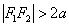 . .
Иными словами, для каждой точки 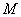 гиперболы модуль разности расстояний гиперболы модуль разности расстояний 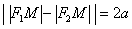 – есть величина постоянная, равная расстоянию между вершинами – есть величина постоянная, равная расстоянию между вершинами
…не очень понятно? – сейчас поправим!
Представьте, что синяя точка 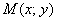 «ездит» по правой ветви гиперболы: «ездит» по правой ветви гиперболы:
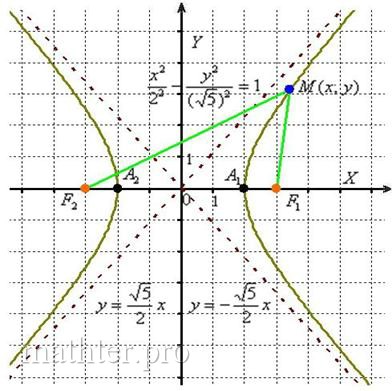 – так вОт, где бы мы ни находились, модуль разности между длинами отрезков – так вОт, где бы мы ни находились, модуль разности между длинами отрезков 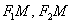 равен расстоянию между вершинами гиперболы: равен расстоянию между вершинами гиперболы: 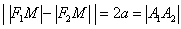
Если точку 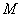 «перекинуть» на левую ветвь и перемещать её там, то данное
значение останется неизменным. «перекинуть» на левую ветвь и перемещать её там, то данное
значение останется неизменным.
Модуль нужен по той причине, что разность длин 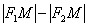 может быть как
положительной, так и отрицательной. Для любой точки правой ветви может быть как
положительной, так и отрицательной. Для любой точки правой ветви 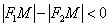 (так
как отрезок (так
как отрезок 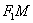 короче отрезка короче отрезка 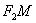 ). Для любой точки ). Для любой точки 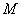 левой ветви
ситуация ровно противоположная и левой ветви
ситуация ровно противоположная и 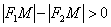 . Более того, ввиду очевидного свойства
модуля . Более того, ввиду очевидного свойства
модуля 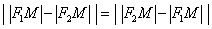 – без разницы, что из чего вычитать. – без разницы, что из чего вычитать.
Удостоверимся, что в нашем примере модуль этой разности действительно равен расстоянию между вершинами 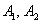 . Мысленно поместите точку . Мысленно поместите точку 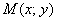 в правую
вершину гиперболы в правую
вершину гиперболы 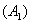 . Тогда: . Тогда:
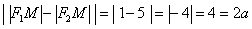 , что и требовалось проверить. , что и требовалось проверить.
Чуть, конечно, всё занятнее, чем с эллипсом, но вполне доступно. Если что-то осталось недопонятым, то вдумчиво перечитайте вышеизложенные абзацы
снова.
 3.4.3. Фокусы и эксцентриситет гиперболы 3.4.3. Фокусы и эксцентриситет гиперболы
 3.4.1. Каноническое уравнение и построение гиперболы 3.4.1. Каноническое уравнение и построение гиперболы
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» – так вОт, где бы мы ни находились,
– так вОт, где бы мы ни находились,  3.4.3. Фокусы и эксцентриситет гиперболы
3.4.3. Фокусы и эксцентриситет гиперболы