3.4.1. Каноническое уравнение и построение гиперболы
Общая структура изложения материала будет напоминать предыдущий параграф. Начнём с общего понятия гиперболы и задачи на её построение.
Каноническое уравнение гиперболы имеет вид 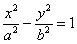 , где , где 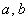 – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие – положительные действительные числа. Обратите внимание, что в отличие от эллипса, здесь не накладывается условие 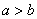 , то
есть, значение «а» может быть и меньше, чем «бэ». , то
есть, значение «а» может быть и меньше, чем «бэ».
Надо сказать, довольно неожиданно… – уравнение «школьной» гиперболы 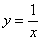 и
близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока раскинем на экране своего воображения график функции и
близко не напоминает каноническую запись. Но эта загадка нас ещё подождёт, а пока раскинем на экране своего воображения график функции 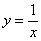 …. Какие мысли? …. Какие мысли?
У гиперболы две симметричные ветви.
У гиперболы две асимптоты.
Неплохой прогресс! Данными свойствами обладает любая гипербола, и сейчас вы с неподдельным восхищением заглянем в декольте этой линии:
Задача 99
Построить гиперболу, заданную уравнением 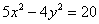
Решение: на первом шаге приведём данное уравнение к каноническому виду 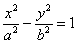 . Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому
обе части исходного уравнения делим на 20: . Пожалуйста, запомните типовой порядок действий. Справа необходимо получить «единицу», поэтому
обе части исходного уравнения делим на 20:
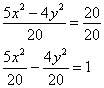
Здесь можно сократить обе дроби, но технически грамотнее сделать каждую из них трёхэтажной (см. Приложение Школьные
материалы):
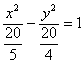
и только после этого провести сокращение:
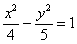
Выделяем квадраты в знаменателях:
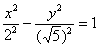
Готово.
Почему преобразования лучше проводить именно так? Ведь дроби левой части 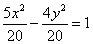 можно сразу сократить и получить можно сразу сократить и получить 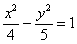 .
Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае получится что-нибудь вроде .
Дело в том, что в рассматриваемом примере немного повезло: число 20 делится и на 4 и на 5. В общем случае получится что-нибудь вроде 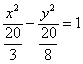 и без 3-го этажа не обойтись: и без 3-го этажа не обойтись: 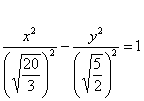 . .
Воспользуемся плодом наших трудов – каноническим уравнением 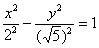 : :
Как построить гиперболу?
Существует два подхода к построению гиперболы – геометрический и алгебраический. С практической точки зрения вычерчивание с помощью циркуля я бы
даже сказал утопично, поэтому гораздо выгоднее вновь привлечь на помощь нехитрые расчёты.
Целесообразно придерживаться следующего алгоритма (читайте и смотрите на чертёж ниже):
1) Сначала находим асимптоты. Если гипербола задана каноническим уравнением 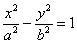 , то её асимптотами являются прямые , то её асимптотами являются прямые 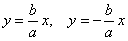 . В нашем случае: . В нашем случае: 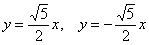 . Данный пункт
обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты. . Данный пункт
обязателен! Это принципиальная особенность чертежа, и будет грубой ошибкой, если ветви гиперболы «вылезут» за свои асимптоты.
2) Теперь находим две вершины гиперболы, которые расположены на оси абсцисс в точках 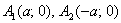 . Выводится элементарно: если . Выводится элементарно: если 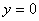 , то каноническое уравнение , то каноническое уравнение 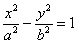 превращается в превращается в 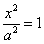 , откуда и следует,
что , откуда и следует,
что 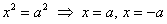 . Наша гипербола имеет вершины . Наша гипербола имеет вершины 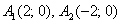
3) Ищем дополнительные точки. Обычно хватает двух-трёх. В каноническом положении гипербола симметрична относительно начала
координат и обеих координатных осей, поэтому вычисления достаточно провести для 1-й координатной четверти. Методика точно такая же, как и при построении эллипса. Из канонического уравнения 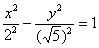 на черновике выражаем: на черновике выражаем:
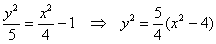
и уравнение распадается на две функции:
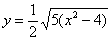 – определяет верхние дуги гиперболы (то, что нам надо); – определяет верхние дуги гиперболы (то, что нам надо);
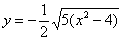 – определяет нижние дуги гиперболы. – определяет нижние дуги гиперболы.
Напрашивается нахождение точек с абсциссами 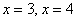 : :
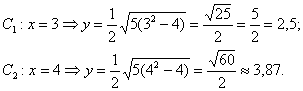
4) Изобразим асимптоты 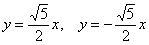 , вершины , вершины 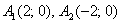 , дополнительные , дополнительные 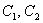 и
симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы: и
симметричные им точки в других координатных четвертях. Аккуратно соединим соответствующие точки у каждой ветви гиперболы:
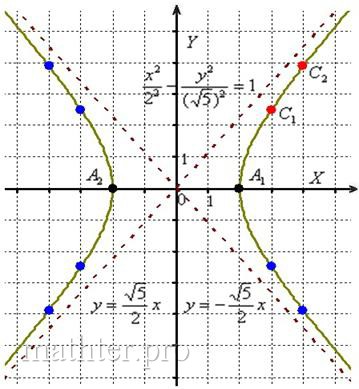 Техническая трудность может возникнуть с иррациональным угловым коэффициентом Техническая трудность может возникнуть с иррациональным угловым коэффициентом 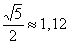 , но это вполне преодолимая проблема. , но это вполне преодолимая проблема.
Отрезок 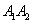 называют действительной осью гиперболы; называют действительной осью гиперболы;
Число 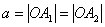 называют действительной полуосью гиперболы; называют действительной полуосью гиперболы;
число 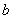 – мнимой полуосью. – мнимой полуосью.
В нашем случае: 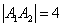 , , 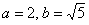 , и, очевидно, если гиперболу повернуть вокруг центра симметрии и / или переместить, то эти значения не
изменятся. , и, очевидно, если гиперболу повернуть вокруг центра симметрии и / или переместить, то эти значения не
изменятся.
 3.4.2. Определение гиперболы 3.4.2. Определение гиперболы
 3.3.4. Поворот и параллельный перенос эллипса 3.3.4. Поворот и параллельный перенос эллипса
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»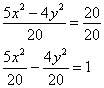
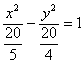
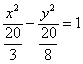 и без 3-го этажа не обойтись:
и без 3-го этажа не обойтись: 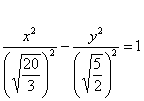 .
.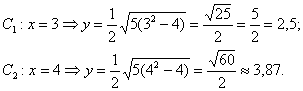
 Техническая трудность может возникнуть с иррациональным
Техническая трудность может возникнуть с иррациональным  3.4.2. Определение гиперболы
3.4.2. Определение гиперболы 3.3.4. Поворот и параллельный перенос эллипса
3.3.4. Поворот и параллельный перенос эллипса