3.3.4. Поворот и параллельный перенос эллипса
Вернёмся к каноническому уравнению эллипса 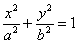 , а именно к условию , а именно к условию 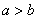 , загадка которого уже давно терзает пытливые умы. Вот мы рассмотрели эллипс , загадка которого уже давно терзает пытливые умы. Вот мы рассмотрели эллипс
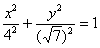 , но разве на практике не может встретиться уравнение , но разве на практике не может встретиться уравнение 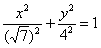 ? Ведь здесь ? Ведь здесь 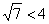 , однако,
это вроде бы как тоже эллипс! И да, это действительно эллипс, развеем мистику: , однако,
это вроде бы как тоже эллипс! И да, это действительно эллипс, развеем мистику:
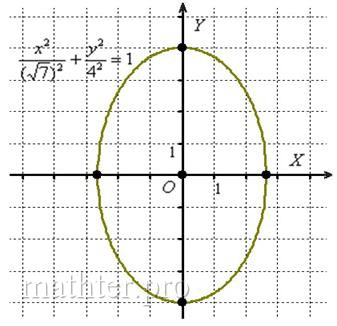 В результате построения получен наш родной эллипс,
повёрнутый на 90 градусов. То есть, В результате построения получен наш родной эллипс,
повёрнутый на 90 градусов. То есть, 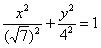 – это неканоническая
запись эллипса – это неканоническая
запись эллипса 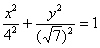 . .
Запись!
– уравнение 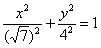 не задаёт какой-то другой эллипс,
поскольку на оси не задаёт какой-то другой эллипс,
поскольку на оси 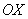 не существует точек не существует точек 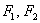 (фокусов), которые бы удовлетворяли определению эллипса. (фокусов), которые бы удовлетворяли определению эллипса.
Как быть, если такой вариант встретился на жизненном пути? В том случае, если вам предложено построить эллипс, то, наверное, лучше построить его в нестандартном виде. С вершинами и дополнительными точками, думаю, трудностей не возникнет. Но если
требуется найти фокусы, эксцентриситет и т.д., то настоятельно
рекомендую начать (или продолжить после чертежа) решение примерно так:
«Повернём эллипс на 90 градусов и перепишем его уравнение 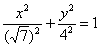 в
каноническом виде в
каноническом виде 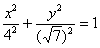 » – дальше по обычной схеме. » – дальше по обычной схеме.
Впрочем, эрудиты могут встать на скользкий путь путаницы, модифицировав все расчёты с учётом поворота. Но всё равно не советую. Ведь эллипс можно
повернуть и на другой угол =)
! Примечание: в теории принято поворачивать не саму фигуру, а оси! И если от вас требуется именно ПРИВЕСТИ уравнение к каноническому
виду, то решение, строго говоря, следует оформить иначе: «Перейдём к новой прямоугольной системе координат 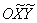 , повернув координатные оси на 90 градусов против часовой стрелки, и запишем уравнение эллипса в
каноническом виде: , повернув координатные оси на 90 градусов против часовой стрелки, и запишем уравнение эллипса в
каноническом виде: 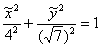 ». ».
В практических задачах чаще встречается параллельный перенос эллипса:
Уравнение 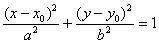 задаёт эллипс с большой полуосью «а», малой полуосью «бэ» и
центром симметрии в точке задаёт эллипс с большой полуосью «а», малой полуосью «бэ» и
центром симметрии в точке 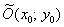 . .
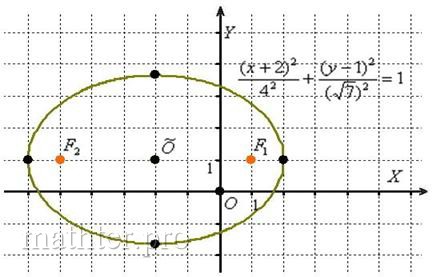
Изобразим на чертеже эллипс 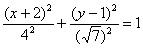 . Согласно формуле, . Согласно формуле, 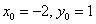 и наш подопытный эллипс вполне комфортно «устроился» в точке и наш подопытный эллипс вполне комфортно «устроился» в точке 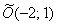 . .
Значения 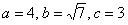 остались прежними, а вот фокусы, разумеется, «уехали» вместе с
эллипсом, и их координаты придётся находить с поправкой на соответствующие сдвиги (расчёты справа): остались прежними, а вот фокусы, разумеется, «уехали» вместе с
эллипсом, и их координаты придётся находить с поправкой на соответствующие сдвиги (расчёты справа):
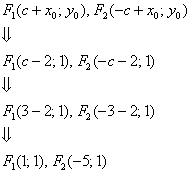
Здесь всё обходится значительно проще, чем при повороте, и если по условию не нужно приводить уравнение к каноническому виду, то лично я
предпочту оставить его в виде 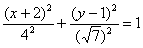 . Что делать, если приводить нужно?
«Чайникам» в большинстве случаев простят фразу: «Осуществим параллельный перенос эллипса в начало координат и перепишем уравнение . Что делать, если приводить нужно?
«Чайникам» в большинстве случаев простят фразу: «Осуществим параллельный перенос эллипса в начало координат и перепишем уравнение 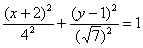 в каноническом виде: в каноническом виде: 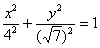 ». Но строгий подход предполагает параллельный перенос не самой фигуры, а координатных
осей! Поэтому людям, изучающим математику углублённо, гораздо лучше сказать примерно следующее: «С помощью параллельного переноса
системы ». Но строгий подход предполагает параллельный перенос не самой фигуры, а координатных
осей! Поэтому людям, изучающим математику углублённо, гораздо лучше сказать примерно следующее: «С помощью параллельного переноса
системы 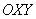 перейдём к новой прямоугольной системе координат перейдём к новой прямоугольной системе координат 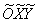 с началом в точке с началом в точке 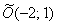 ,
и запишем уравнение эллипса в каноническом виде ,
и запишем уравнение эллипса в каноническом виде 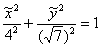 ». ».
На самом деле с упрощённой версией рассматриваемой формулы мы знакомы ещё со школьных времён: уравнение 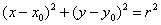 задаёт окружность радиуса задаёт окружность радиуса 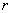 с центром в точке с центром в точке 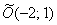 . .
Освежая ностальгические воспоминания, изобразим на чертеже окружность, заданную уравнением 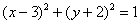 : :
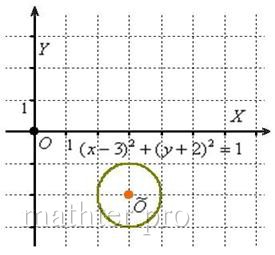 В исследовательских целях приведём это уравнение к общему
виду. Выполним возведение в квадрат по формулам В исследовательских целях приведём это уравнение к общему
виду. Выполним возведение в квадрат по формулам 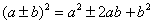 и приведём подобные
слагаемые: и приведём подобные
слагаемые:
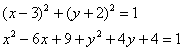
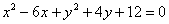 – как правило, в таком обличье уравнение и встречается в природе. – как правило, в таком обличье уравнение и встречается в природе.
И в практических задачах часто нужно выполнить обратное действие – выделить полные квадраты, «сконструировав» трёхчлены и
применив формулы в обратном порядке: 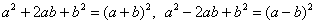 . .
Выполняем это креативное задание самостоятельно:
Задача 98
Построить график линии, заданной уравнением 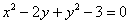
Решение и чертёж в конце книги.
На практике эллипс (как, впрочем, и другая линия) может быть одновременно повёрнут на любой угол относительно своего
канонического положения и перенесён в любую точку, отличную от начала координат. В таком случае решается более трудная версия задачи приведения линии 2-го порядка к каноническому виду, к которой я потихоньку начал вас готовить уже сейчас.
 3.4.1. Гипербола 3.4.1. Гипербола
 3.3.3. Эксцентриситет эллипса и его геометрический смысл 3.3.3. Эксцентриситет эллипса и его геометрический смысл
| Оглавление |
|

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников» В результате построения получен наш родной эллипс,
повёрнутый на 90 градусов. То есть,
В результате построения получен наш родной эллипс,
повёрнутый на 90 градусов. То есть, 
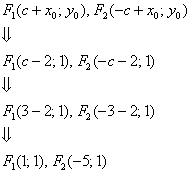
 В исследовательских целях приведём это уравнение к общему
виду. Выполним возведение в квадрат по формулам
В исследовательских целях приведём это уравнение к общему
виду. Выполним возведение в квадрат по формулам 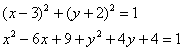
 3.4.1. Гипербола
3.4.1. Гипербола 3.3.3. Эксцентриситет эллипса и его геометрический смысл
3.3.3. Эксцентриситет эллипса и его геометрический смысл