|
Ваш репетитор, справочник и друг!
|
3.3.3. Эксцентриситет эллипса и его геометрический смыслЭксцентриситетом эллипса называют отношение Выясним, как форма эллипса зависит от его эксцентриситета. Для этого зафиксируем левую и правую вершины эллипса (грубо говоря,
ширина эллипса будет оставаться постоянной). У рассматриваемого эллипса (см. рис. выше) большая полуось равна Начнём приближать значение эксцентриситета к единице. Это возможно только в том случае, если Таким образом, чем ближе значение эксцентриситета эллипса к единице, тем эллипс более продолговат. Теперь смоделируем противоположный процесс: фокусы эллипса При этом отрезкам Таким образом, чем ближе значение эксцентриситета к нулю, тем эллипс всё больше похож…, смотрим на предельный случай И действительно, в случае равенства полуосей каноническое уравнение эллипса На практике чаще используют запись с «говорящей» буквой «эр»: Заметьте, что определение эллипса остаётся полностью корректным: фокусы совпали Строится окружность легко и быстро, достаточно вооружиться циркулем. Тем не менее, иногда бывает нужно выяснить координаты некоторых её точек, в
этом случае уравнение После чего подставляем нужные значения «икс» и получаем «игреки». Творческое задание для самостоятельного решения, а то как-то вы расслабились:) Задача 97 Составить каноническое уравнение эллипса, центр которого находится в начале координат, если известен один из его фокусов Решение и чертёж в конце книги
|
|
© mathprofi.ru - mathter.pro, 2010-2026, сделано в Блокноте. |

 Аналитическая геометрия для «чайников»
Аналитическая геометрия для «чайников»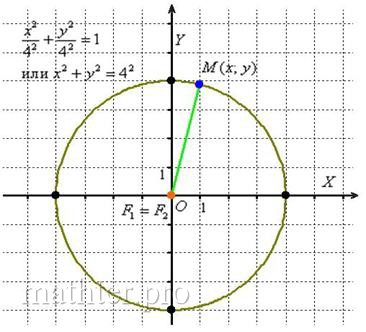 Окружность – это частный случай эллипса.
Окружность – это частный случай эллипса. 3.3.4. Поворот и параллельный перенос эллипса
3.3.4. Поворот и параллельный перенос эллипса 3.3.2. Определение эллипса. Фокусы эллипса
3.3.2. Определение эллипса. Фокусы эллипса